Решението, с интервали неравенства

1. По-широкото използване на метода на интервалите за решаване на неравенства
2. Показване на възможностите на този метод за решаване на неравенства, съдържащи променливи под знака на дневника и тригонометрични функции.

Ще разгледаме неравенството, от дясната страна е равна на нула, а в лявата част е представена под формата на продукт или частни мероприятия.

Идеята на метода: Знакът на работата или в частния, така определя от знака на факторите.

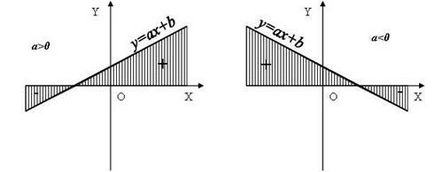
Линейна функция с ненулев наклон променя знак при преминаване през нулата на функцията, с право на функцията на нула марка съвпада със знака на наклона.

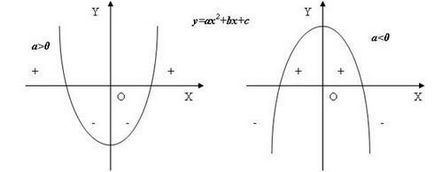
Square трином с D> 0, когато преминава през всяко нула на функцията променя знак, с норма на квадратен корен знак трином на съвпада с водещата си коефициент. [1]

Тези съображения водят до следното неравенство схемни решения:

1. Намираме нули на числителя: ,,.
2. Ние считаме, нулите на знаменателя :.
3. Начертайте Point нули върху реалната ос. защото неравенство е строг, а след това всички нули изобразяват пробиви, които разграждат по цифровите ос интервали:

От дясната страна са знака на всеки фактор съвпада с водещата си коефициент:

Следователно, фракцията на тази разлика е отрицателен.

1. При преминаване през всяка от маркирани нула, един и само един фактор промени подпишат, и така всеки път, когато стреля марка. С оглед на това, ние поставяме в интервалите на знаци (както е показано на Фигура 3).
2. Изберете интервалите, през които фракцията е отрицателна.
3. Напишете отговора.

В примера 1, знаците в интервалите на постоянните функции знак заместници. Въпреки това, за да се обобщи, че това винаги ще се случи, разбира се, не трябва да бъде.

-2 - нула секунди множество

ние поставяме нули намерени на реалната ос, тъй като неравенството не е строг, а след това на нули на числителя представлявана от сенчестите точките, както и изчезването знаменателя ние, пункции, защото този брой не е включена в областта на неравенството:

Са нула секунди кратност кърлеж, да не забравя. защото числителят е винаги отнема положителни стойности, а след това най-дясната характер интервал ще зависи от знака на водещи коефициента на знаменателя, т.е. "+". Вляво от "1" е отрицателен знаменател и числителят положителен, следователно, когато преминават през цифрите -2 знак не се променя:

Това ще помогне да се разбере следното геометрична изображение (Фигура 6):

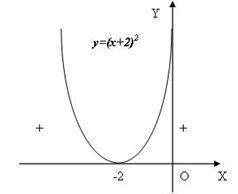
1. За да запишете отговора избере една празнина, където има знак "+" и сенчести точка, при която част е нула.
   отговори на:

Заключение: прехода през нулата дори кратност, знакът не се променя.

За решаването на вариантите, последвани от дискусия в борда.

1. нули на числителя:
   - нула секунди множество

нули на знаменателя:

;
- третата нула на множество

метод интервали на приложения не се ограничава само до решението на рационални неравенства.

Универсалността на метода се основава на достатъчно визуален собственост на непрекъснатост, "Ако интервалът (а, б) функция F (х) е непрекъснато и не стане нула, тогава този интервал запазва подпише."

Ние ще решим този неравенство по същата схема, но по цялата линия, а на домейна на логаритмична функция, т.е. в интервала (*):

Следователно в този интервал лява страна е отрицателен

1. при преминаване през всеки корен променя знака на един и само един от факторите. Като се има предвид това, ние поставяме знаците в оставащите пропуски.

нули на знаменателя:

разтворът е изобразен на фиг. 10:

Square трином в числителя още няма корени и не променя своя знак. Неговият знак съвпада със знака на водещия коефициент, т.е. "+".

Ние даваме на този вид неравенство в дясната страна е "0":

1. нули на знаменателя:
   
2. разтворът е изобразен на фиг. 11:

, но само отговаря на ДХС

1. разтворът е изобразен на фиг. 13:

дом задача (решение, предоставена в Приложение 1),

Задачи за извънкласни дейности, предвидени в Prilozhenii2.

Заключение: Както е известно, линейни, квадратичен, експоненциални, експоненциални, логаритмични и тригонометрични функции, както и техния състав и функции, получени от тях чрез аритметични операции са непрекъснати на потребителите. Следователно, методът на интервали може да се използва при решаване на почти всички неравенства училище разбира се. интервали настоящото метод позволява множество разтвори на неравенство като обединение на интервали, чиито граници или корените на уравнението или гранични точки на определение.

[1] // списание "интервал метод" "Quantum" No12, 1985