Аксонометрично проекция, cadinstructor
В много от случаите, когато техническите чертежи е полезен, заедно с образа на обекти в системата на проекции да има визуален образ. За се използват изграждането на прожектираните изображения, наречена перспектива.
Метод аксонометрична проекция е, че обект заедно с осите на декартови координати, за които тази система принадлежи в пространството, паралелно проектирана върху равнина α (фигура 4.1).
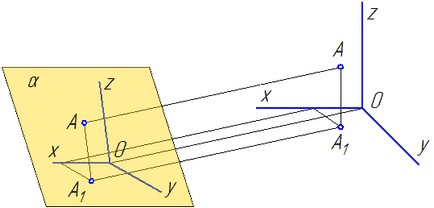
посока проекция S определя позицията на оси аксонометрични проекции на равнина алфа на. както и фактори ги нарушава. Необходимо е да се гарантира видимостта на изображението и възможността за производство на определени позиции и размери на даден обект.
Като пример, Фигура 4.2 показва конструкцията на аксонометрична проекция на точка А на своите ортогонални проекции.
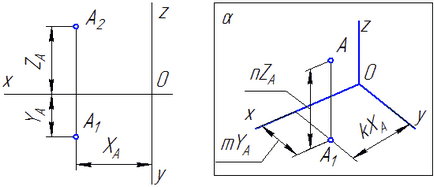
Ето, к букви. м. п означават изкривяване коефициенти на говедото на оси. OY и OZ съответно. Ако и трите фактора са равни, то се нарича изометрично гледна точка, ако равни само две коефициенти, проекцията се нарича dimetric. ако к ≠ m ≠ п. проекцията се нарича Trimetric.
Ако посоката на проекция S перпендикулярна издатини равнина алфа. изглед в перспектива е името на квадрат. В противен случай, перспектива прогнозен се нарича наклонена.
- правоъгълна и изометричен dimetric;
- предна изометричен наклонена, хоризонтална и предна изометричен dimetric;
По-долу са единственият от трите най-често използваните в практиката, аксонометрични проекции.
Всяка такава проекция ос, определени от позицията, изкривяване коефициенти на тях, размерите и посоки на осите на елипсите разположени в равнини, успоредни на координатните равнини. За опростяване на геометричната изкривяване конструкции коефициенти оси обикновено са закръглени.
4.1. правоъгълни проекции
4.1.1. изометрични
Посока аксонометрични оси е показано на фигура 4.3.
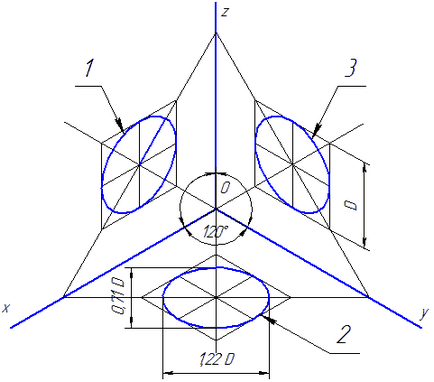
Фигура 4.3 - аксонометричен ос в правоъгълна изометричен
Действителни изкривяване коефициенти на говедото на оси. OY и OZ равно на 0.82. Но с такива стойности на коефициентите на изкривяване не е удобно да се работи, така че на практика, тъй като изкривяването се използват коефициенти. Тази проекция обикновено се извършва без изкривяване, обаче, намалява коефициентите на деформация се вземат к = m = п = 1. Обиколка разположена в равнини, успоредни на равнините на проекция, проектирани в елипси, чиято основна ос е равно на 1.22. и малък - диаметъра на окръжността на 0,71 D.
Основните оси на елипсите 1, 2 и 3 са разположени под ъгъл от 90 ° към оста OY. OZ и ОХ. съответно.
Едно примерно изпълнение на изглед в перспектива с изрязани части условие е показана на Фигура 4.4.
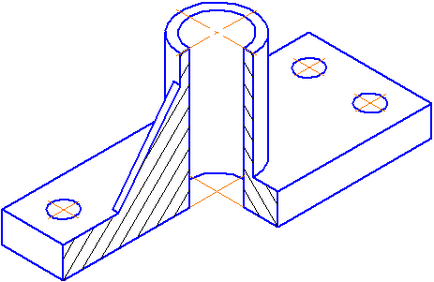
Фигура 4.4 - Подробности картина в правоъгълна изометричен
4.1.2. dimetric проекция
Правило се извършва аксонометрични оси на Фигура 4.5.
За да се конструира ъгъл приблизително равна 7º10. вграден правоъгълен триъгълник, чиято катетите са един и осем единици на дължина; за конструиране на ъгъл приблизително равна 41º25 '- краката на триъгълника, респективно, равна на седем и осем единици на дължина.
Коефициентите на нарушаването на осите вол и OZ к = п = 0,94 и на оста OY - m = 0,47. Когато закръгляване е взето от тези параметри К = п = 1 и m = 0,5. В този случай размерите на оси на елипсите са: главната ос е равно на 1 и елипси 0,95D 2 и 3 - 0,35D (D - диаметър на кръга). На Фигура 4.5 главната ос 1, 2 и 3 са разположени под ъгъл от 90 ° към оста OY, OZ и OX, съответно.
Пример dimetric правоъгълна проекция условни части разрез е показан на Фигура 4.6.
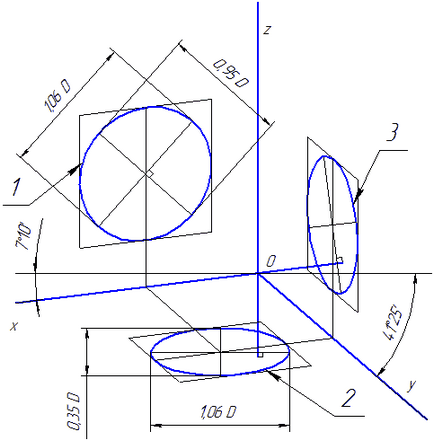
Фигура 4.5 - аксонометричен ос в правоъгълна проекция dimetric
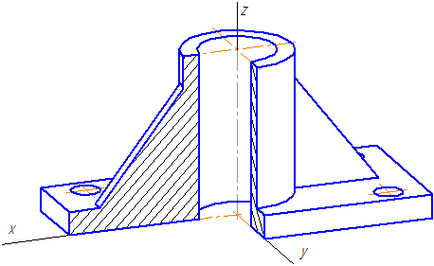
Фигура 4.6 - Подробности картина в правоъгълната проекция dimetric
4.2 косо проекция
4.2.1 Предна проекция dimetric
Регламент аксонометрични оси е показано на фигура 4.7. Dimetric оставя да се използва ъгъл на предната проекция на оста OY 30 0 и 60 0.
изкривяване коефициент OY ос е т = 0,5 и осите OX и Оз - К = п = 1.
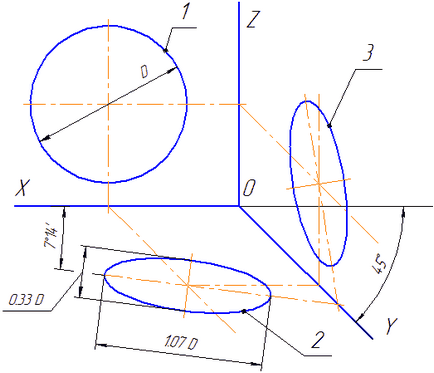
Фигура 4.7 - аксонометричен ос в проекция dimetric наклонена предна
Обиколка разположена в равнини, успоредни на челната равнина на проекция, проектира върху равнина XOZ без изкривяване. Основните оси на елипсите са равни на 2 или 3 1,07D. и малка ос - 0,33D (D - диаметър на кръга). Главната ос 2 прави с ъгъл на наклона на оста х 7 ° 14 '. и главната ос 3 на същия ъгъл с оста Оз.
Пример аксонометричен условни части разрез е показан на Фигура 4.8.
Както се вижда от фигурата, част е разположен така, че обиколката си проектира върху равнина XOZ, без изкривяване.
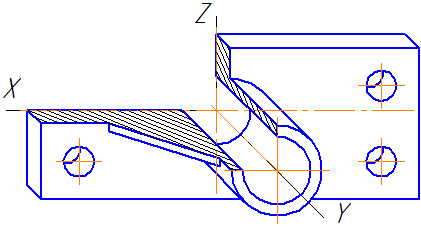
Фигура 4.8 - данни на изображението в проекция dimetric наклонена предна
4.3 Изграждане на елипсата
4.3.1 на елипсата в две оси
елипса данни оси АВ и CD са конструирани като две концентрични кръгове диаметри (фигура 4.9, а).
Един от тези кръгове е разделена на няколко равни (или неравни) части.
Чрез точките на разделяне и центъра на радиусите на елипса се провеждат, които са разпределени като втори кръг. След това, през големия кръг разделителни точки се проведе права и успоредна на линията AB.
пресечните точки на съответните линии и точки ще са собственост на елипса. На Фигура 4.9 А показва само една желана точка 1.
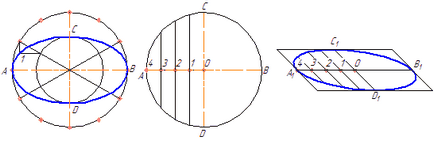
Фигура 4.9 - Изграждане на елипсата в две оси (А) на гредите (б)
4.3.2 Изграждане на елипсата от акорди
Диаметърът на кръга AB е разделена на няколко равни части, Фигура 4.9, б 4. Чрез техните точки 1-3 се провеждат паралелно CD диаметър акорд. Във всеки аксонометрична проекция (например, в полегато dimetric) са представени с еднакви диаметри с коефициент на изкривяване. Така на фигура 4.9, б = AB А1 В1 и С1 D1 = 0,5CD. Диаметър А1 В1 е разделена на същия брой равни части, диаметър AB на, 1-3 чрез точките от данните, съхранявани сегменти са, съответно, струни, умножени с нарушаването на коефициента (в нашия случай - 0.5).
4.4 Люпене на секции
Линии люкови секции (Прорезите) в аксонометрични проекции се прилагат паралелно една на диагоналите на квадрата, лежащи в съответните координатни равнини, от двете страни на който са успоредни на осите на перспективен (Фигура 4.10: А - в правоъгълна засенчване изометричен б - челната наклонена люпене в диаметър).
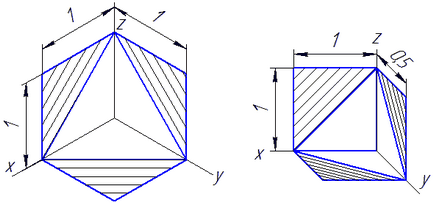
и б
Фигура 4.10 - Примери за люпене в аксонометрични проекции