Циклична структура - studopediya

(. Фигура 1.3) Отличителна черта на тази структура е присъствието в състава си:

- част многократно с многократно по време на изчисления и нарича линия на тялото; тялото е типичен линейна или разклонена структура;

- състояние L, предназначени за ранно излизане от цикъла.

Циклични структури са два вида: с предпоставката, че е, проверка условия контур изходни преди изпълнение тялото (а) и postcondition, от което предполага по-горе състояние след извършване линия тяло (б).

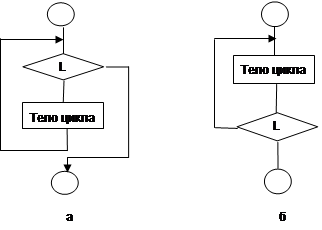
Фигура 1.3. Сортовете на циклични структури:

а) предпоставка; б) с postcondition

Циклични структури се използват като отделни елементи в развитието на алгоритми за изчисляване на циклични процеси (цикли). Разграничаваме:

1) цикъла с известен брой повторения на тялото или броя на повторенията, които могат да бъдат оценени. Тези цикли се наричат ​​аритметика (преброяване).

2) броя на повторения на цикъла на който не е предварително известна и не може да се изчисли - повтарящи се цикли.

Как да стигнем до организацията на цикъла, трябва да:

- определи коя променлива ще го ръководи, или, както се казва, да служи egoparametrom;

- да формулира закона за изменение на параметъра, т.е. определите как стойността му ще се промени след всяко повторение на тялото;

- определяне на цифровата стойност, при която трябва да се предоставя на изхода от цикличен процес.

Да разгледаме примери за циклични алгоритмични процеси изчисляване, посочени в претенция 1.

Нека функция у = греха (х2). Необходимо е да се изчисли стойността му в интервала [а, б], ако аргумент х се променя на този сегмент от доста специфични, предварително определени, законно. Тъй като законът на изменение на аргумента, ние избираме най-простите, но в същото време и често се използва от закона

където Dx е величината, която се нарича стъпка на аргумента. Замествайки стойностите на предходната Формула I, получаваме:

т.е. всеки следващ стойност на аргумент х се изчислява чрез сумиране на предишната стойност го инкрементира Dx (фигура 1.4). Проблемът формулирани по такъв начин се нарича проблема на таблица функция.

Сега е ред на развитието на алгоритъма. През този проблем, управляема променлива (параметър цикъл) е аргумент функция, защото на сегашната си стойност зависи от решение на въпроса дали да продължи по-нататъшното изпълнение на изчислителни контур или край и да се измъкнем от него.

Ако следващата аргумент стойност е в интервала [а, б], цикълът се повтаря, докато изчисляване на съответната стойност на функцията, в противен случай излизане от цикъла.

Тъй като промяната на параметъра, изложени в декларацията на проблема, той остава да се определи стойността, при която цикличен процес трябва да бъде завършена. Очевидно е, че тази стойност се определя от неравенството XI> б.

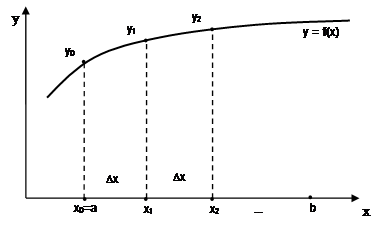
Фиг. 1.4. Геометричната смисъла на функцията за задача таблични

Забележка. Ако първоначалната стойност на аргумента е етап Ь и неговата промяна е отрицателен, тогава състоянието на цикъла изход е неравенство XI

Ние създаваме един алгоритъм на нашата задача, въз основа на следното:

- първоначалната стойност на изчислимо функцията аргумент е известен от състоянието на проблема х = 0 а, следователно, е възможно веднага да се изчисли съответната стойност на функция у 0.

- още една стъпка - линия маса изход, съдържащо стойностите на аргумента и функцията;

- допълнително изчисляване на следващата стойност на аргумента, използвайки правото на промени върху реалната ос XI + 1 = XI + Dx;

- аргумент стойност, получена XI сравнение с края му стойност б; Ако се окаже, че XI> б, а след това завърши с проблема, а ако не - да пристъпи към изчисляване на функцията на следващата стойност.

Ние представлява алгоритъм, както е описано вериги и компактен.

Подробен график