Докажете, каква е площта на успоредник

Площта на успоредник е равна на произведението на една ръка на високо, извършена от страната. Сиде, към която се проведе на височината, която се нарича основа. Затова формулират теоремата, както следва: в района на успоредник е равна на произведението на основата на височината.

Обозначаващ база успоредник писмо А, височината - буквата Н, тогава областта се изразява с формулата:

Имайте предвид, че тази формула е много подобен на площта на правоъгълник, където тя е равна на страната на продукт. Въпреки това, в случай на успоредник, вместо да се използва височина втора ръка. И това трябва да се вземе, че височината, която се провежда в страна, която се приема като множител.

За да се докаже теоремата на зоната на успоредник по два начина: чрез площта на триъгълника, чрез областта на правоъгълник. Помислете за първия случай.

Нека успоредник ABCD, където споменатият ъгъл А - остър и ъгъл Б - тъп. В такъв случай на страничен АД на височината задържане на ъгъла B BH, тя пресича страна на АД. Ако височината е извършена на ъгъл С, това не би пресякъл страна АД и неговото разширение извън успоредника. Също така ъгъл В на теглене диагонал.

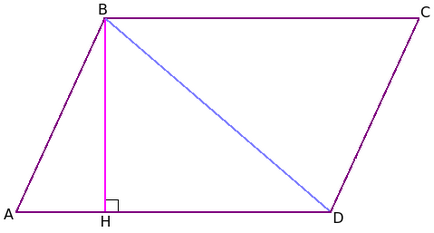
След като прекара диагонал, имаме триъгълника ABD. Тя е с площ, равна на половината от своето основаване височинни работи. В този случай, на ½ * * АД BH. Доказателство площ на триъгълник е дадено тук.

Тъй като BD диагонал разделя на две равни успоредника триъгълници (ΔABD = ΔCDB от три страни), неговата площ е равна на два пъти площта на всяко от тези триъгълници (или сумата от техните области). По този начин ние виждаме, че площта на успоредник е равна на АД * BH, т. Е. Продуктът на основата и височината.

Вторият начин за доказване - чрез разглеждане на правоъгълника. Начертайте АД към базата в две височини. Един от тях (BH) пресича самата база, а втората (CI) - продължаване на АД основания извън успоредник (пресича линията, на която е АД).

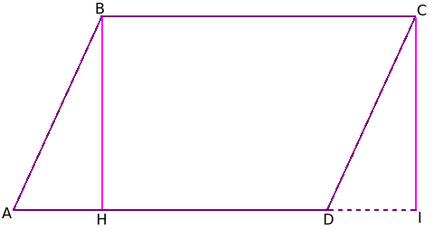
Помислете за триъгълници ABH и ЦРУ. Те са равни един на друг (например от ъглите на хипотенузата и лоши и CDI). Ако ние считаме, в резултат на правоъгълник HBCI, виждаме, че на площ, равна на площта на успоредника на ABCD, тоест. А. конвертиране на първата във втората, в успоредник "лишен" зона на ABH, а по-късно добавя към него равна на площта на директора на ЦРУ.

Районът е продукт на своите страни. В този случай BH * HI. HI, но можем да се замени с АД, тъй като тя е равни отсечки. По този начин ние откриваме, че областта на правоъгълник е равно на BH * АД. Тъй като районът на успоредник и правоъгълник са равни, а след това тази работа е в областта на успоредник.