Функции дефинирани по параметри

Да разгледаме базовата линия в равнината, в която заместителите X, Y са функции на трети вариабилен T (известен параметър):

За всяка стойност на тон в някои интервал отговаря на определени стойности на х и у, а. Следователно, определен момент М (х, у) равнина. Когато т варира над всички стойности на определения интервал, тогава точка М (х, у) описва някои линия L. Уравненията (2.2) се наричат ​​параметри уравнения линия L.

Ако функция х = # 966 (т) е обратен Т = F (х), след това се замества този израз в уравнение у = г (т), ние получаваме у = грам (F (х)), която Y определя като функция на х. В този случай казваме, че уравнението (2.2) определя функция у параметрично на.

ПРИМЕР 1 Нека М (х, у) - произволна точка на окръжност с радиус R и центрирано в основата. Нека т - ъгълът между оста Ox и радиуса ОМ (виж фигура 2.3.).. Ако х, у са изразени с т:

Уравнения (2.3) са параметрични уравнения обиколка. Ние изключат от уравнения (2.3), параметър Т. За тази цел всяка от уравнения ние квадрат и се добавя, ние получаваме: х 2 + Y 2 = R 2 (COS 2т + грях 2т) или х 2 + Y 2 = R 2 - уравнение на окръжност в Декартова координатна система. Той определя две функции: Всяка от тези функции е даден от параметрични уравнения (2.3), но за първата функция. и за втори.

Пример 2. уравнението параметри

определи елипса с полу-оси А, В (фиг. 2.4). Премахването уравнения параметър т. Ние получи каноничното уравнение на елипса:

ПРИМЕР 3 циклоида нарича линия, описана точка лежи на кръг, ако този кръг ролки без приплъзване върху правата линия (фиг. 2.5). Представяме на параметричните уравнения на Циклоида. Нека радиуса на търкаляне кръга е равен на една. точка М. описващ Циклоида, в началото на движението съвпада с произхода.

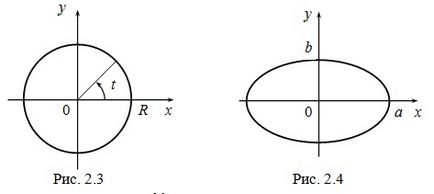
Ние дефинираме координатите х. М у точка след Диаметърът на ъгъл т
(Фиг. 2,5), т = ÐMCB. MB дължината на дъгата, равна на дължината на OB на сегмента, като кръг ролки без подхлъзване, така че

OB = в, AB = р = asint, CD = acost, х = OB - AB = най - asint = а (т - Sint),

у = AM = CB - CD = а - acost = а (1 - стойност).

Така полученото параметрични уравнения на Циклоида:

Когато параметър Т от 0 до обиколката 2π се върти една страна, точка M описва циклоида арка. Уравнения (2.5) се определя като функция на Y от х. Въпреки че функцията X = а (т - Sint) има функция обратен, но не може да се изрази чрез елементарни функции, така че функция у = F (х) не може да бъде изразена по отношение на елементарни функции.

Да разгледаме деривация функция дава от параметрични уравнения (2.2). функцията X = # 966; (Т) промени в определен интервал т има обратна функция Т = F (х). тогава Y = грам (F (х)). Нека х = # 966 (т). у = грам (т) са получени, където x't ≠ 0. Според правилото за диференциране съставна функция y'x = y't х t'x. Въз основа на правилата на диференциация на обратните функции. Ето защо:

Получената формула (2.6), дава възможност да се намери на производно на функцията дефинирани параметрично.

Пример 4. Нека функция у. в зависимост от х. зададат параметри:

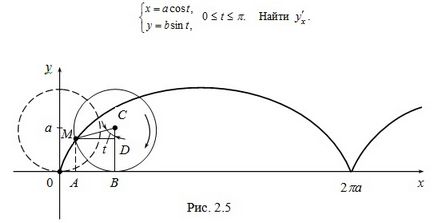
Решение. ,
Пример 5. Намерете ъглов коефициента на допирателната към циклоид точката M0. съответстващ на стойността на параметъра.
Решение. От циклоидални уравнения: y't = asint, x't = а (1 - разходите), следователно

Наклонът на допирателната в точка m0 е стойността на t0 = π / 4:

Нека функцията в точка x0 на е производно. По дефиниция:
Ето защо, на граничните свойства (Sec. 1.8). където - когато една мъничка # 916 х → 0. Следователно,

# 916; Y = F "(x0) # 916 х + # 945; х # 916 х. (2.7)

при # 916 х → 0, вторият в уравнение (2.7) е безкрайно по-висок порядък, в сравнение с. следователно # 916; Y и F '(x0) х # 916 х - еквивалент безкрайно малък (ако е "(x0) ≠ 0).

Така, функцията за увеличение # 916; Y е съставен от две думи, първият от които е "(x0) х # 916 х е нарастване на основната част # 916; у, относително линейно # 916 х (ако е "(x0) ≠ 0).

Диференциална функция е (х) при x0 е основната част на функцията на нарастване и означен: ди или DF (x0). Ето защо,

DF (x0) = F '(x0) х # 916 х. (2.8)

Пример 1. Виж функцията диференциална ди и функцията за увеличение # 916 у за функция у = х 2 от:
1) на произволна и х # 916 х; 2) x0 = 20, # 916 х = 0,1.

1) # 916; у = (х + # 916 х) = 2x 2 х 2 + 2х # 916 х + (# 916 х) 2x 2 = 2x # 916 х + (# 916 х) 2. ди = 2x # 916; х.

2) Ако x0 = 20, # 916 х = 0,1, тогава # 916; у = 40 х 0,1 + (0,1) 2 = 4,01; Dy = 40 х 0,1 = 4.

Пишем уравнението (2.7), под формата на:

# 916; у = Dy + с х # 916 х. (2.9)

увеличаване # 916 у ди диференциална различава от безкрайно от по-висок порядък в сравнение с # 916; х, така че в приблизителни изчисления са приблизителни равенство # 916 у ≈ Dy, ако # 916 х е достатъчно малък.

Като се има предвид, че # 916; Y = F (x0 + # 916 х) - F (x0), ние получаваме приблизителната формула:

Пример 2. Изчисли приблизително.

С помощта на уравнението (2.10), ние получаваме:

.

Така че, ≈ 2025.

Разглеждане на геометрична значение DF (x0) на разлика (фиг. 2.6).

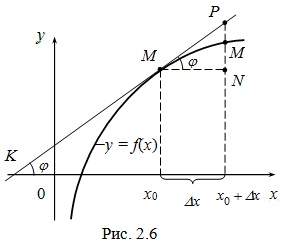
За да се направи графика на функция у = е (х) допирателната в точката M0 (x0, F (x0)), нека # 966; - ъгълът между допирателната и KM0 Ox ос, след което е '(x0) = TG # 966. от # 916; M0NP:
PN = TG # 966; х # 916 х = F '(x0) х # 916 х = DF (x0). Но PN му постепенно се координира тангента промяна на х от x0 да x0 + # 916 х.

Следователно разлика от F функция (х) при x0 е равна на допирателната на нарастване ордината.

Намираме разлика от функцията
у = х. Тъй като (X) '= 1, тогава DX = 1 х # 916 х = # 916 х. Ние приемаме, че разлика от независима променлива х е равно на неговото нарастване, т.е. DX = # 916 х.

Ако х - произволен брой, от (2,8) получаваме DF (х) = F '(х) DX, където.
По този начин, производно на функция у = F (х) е съотношението на разликата на разлика на довод.

Помислете за свойствата на диференциалната функция.

Ако ф (х), о (х) - диференцируема функция, след това по следната формула:

За да се докаже тези формули се използват производни с формула за сумата, продукт, и частни функции. Ние показваме например, формула (2.12):

г (ф х о) = (ф х х) "# 916 х = (ф х о '+ U" х о) # 916 х = ф х о' # 916 х + U '# 916 х х V = ф х DV + V х дю.

Да разгледаме комплекс диференциална функция: у = е (х), х = # 966 (т), т.е. Y = F (# 966 (т)).

че x't = DX, получаване на ди = y'x DX = F '(х) DX.

По този начин, диференциална функция на функция у = е (х), където х = # 966 (т), се дава от ди = F '(х) DX, същите, както в случая, където х е независима променлива. Това свойство се нарича диференциална форма инвариантността и.