Какво е неразделна и какво е неговото физическо значение

Външният вид е концепцията за неразделна поради необходимостта от намиране на примитивна функция на неговите производни, както и определяне на стойността на работата площ сложни форми, изминато разстояние разстояние, с параметрите, очертани извивки от нелинейни уравнения.

разбира се

и физиката знаем, че работата е продукт на сила при големи разстояния. Ако всичко, движението е с постоянна скорост или разстояние се преодолее с прилагането на една и съща сила, тогава всичко е ясно, просто се умножават. Какво е интеграл от константа? Това е линейна функция на форма Y = KX + C.

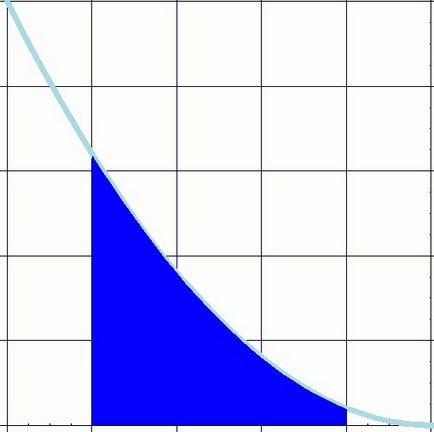
Но силата на работа може да се променя и в някои отношения подреден. Подобна ситуация възниква с изчисляването на изминатото разстояние, ако скоростта не е постоянна.

Така че, това е разбираемо защо е неделима. определяйки го като сбор от продукти на стойностите на функцията на безкрайно нарастване на аргумента, напълно описва основното значение на термина като площта на фигурата, ограничена от най-горния ред на функцията, а по краищата - определянето на граници.

Жан Гастон Darboux, френски математик, през втората половина на ХIХ век е много ясно обясни, че това неразделна. Той направи това толкова ясно, че цяло няма да е трудно да се разбере дори ученик прогимназията по този въпрос.

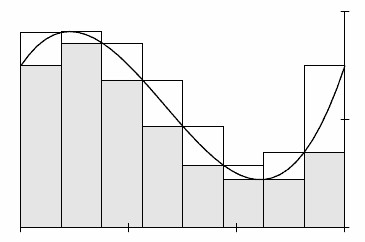
Да предположим, че е функция на сложна форма. ордината, върху които е образувана стойността на аргумента, се разделя на малки интервали от време, в идеалния случай, те са безкрайно малко, но тъй като концепцията за безкрайността е доста абстрактно, то е достатъчно, за да си представим само малки парчета, размерът на които обикновено се означава с гръцката буква делтата (делта).

Функцията е "нарязан" на по-малки блокове.

Всяка стойност на аргумента съответства на точка на ординатната ос, при която депозиран съответните стойности на функцията. Но, тъй като границите в избраната област две, ценностите и функции ще бъдат две или повече и по-малко.

Сумата от продукти на големи стойности за нарастване δ Darboux нарича голямо количество, и се означава като S. Следователно, по-малки стойности за ограничена област, умножена по δ, заедно образуват малко количество Darboux S. Самият комплекс прилича на правоъгълен трапец, така че в зависимост от кривината на линията се дължи на нарастване безкрайно могат да бъдат пренебрегнати. Най-лесният начин да се намери областта на геометрична форма - сгънати парчета по-големи и по-малки стойности на функцията на δ инкрементиране и разделете на две, че се определя като средната аритметична стойност.

Това е, което интегралната Darboux:

S = σf (х) δ - малко количество;

S = σf (х + δ) δ - голямо количество.

Така че, това, което е неразделна? Площ, ограничена от линия функция и определяне на границите ще бъде равен на:

Това означава, че средната аритметична стойност на големи и малки количества Darbu.s - постоянна стойност, се нулира при диференциация.

Въз основа на геометричната израз на тази концепция, става ясно, физическия смисъл на интеграла. Квадратни форми, описани функция на скоростта и ограничен интервал от време на оста х ще бъде дължината на изминатото разстояние.

L = ∫f (х) DX в интервала от t1 до t2,

е (х) - функция на скоростта, който е формула, с което се променя с течение на времето;

L - дължина на пътя;

t1 - началния час на пътя;

T2 - краен срок за изпълнение път.

Точно същия принцип се определя от размера на работата, но ще бъдат депозирани по абсцисата разстоянието и ординатата - сумата на сила, упражнена върху всяка отделна точка.