Като определя от големината и посоката на скоростта на мястото координатна референтна метод движение

Начало | За нас | обратна връзка
Какви са начините за уточняване на движението на точка се използва в кинематиката и какви са те? Как да се определи траекторията на пътя, когато точка от работата на координатната?
Точката за движение в пространството се определя от три основни начина: вектор, координира и естествени.
Vector: ние избираме фиксиран център О, и изготвя от центъра на точка М, която проучване движение, радиус-вектора г. При движение на точка М промени радиус вектора в сила и посока. Всяка точка от времето съответства на определена стойност т г. Следователно вектор радиус еднозначно определя позицията на точка М, така че да се определи точката на движение, е необходимо да се вектор радиус под формата на един непрекъснат време функция R: R = R (т).
Ордината: Ако координатните точки се определя като един ценен функция на времето: х = х (т), у = Y (т), Z = Z (т), позицията на точка М в пространството е известно на всеки момент. Тези уравнения определят закона на движение на точка и се наричат уравнения на движението му.
Физически: Този метод се използва в задачата за движение, когато траекторията на точка спрямо избрана координатна система е известна. При преместване на криволинейната координата на точка М те ще варира с течение на времето, което е: S = S (T). Знаейки това уравнение, ние можем да се определи позицията на всеки момент от време. Тя се нарича уравнение на движение и правото на движение по предварително определен път.
Ние дефинираме позицията на точка в координатната пространство на специално: х = х (т), у = Y (т), Z = Z (т) (*). За да се определи позицията на точката на първоначалното време (т = 0) е необходимо в уравнение (*), за да замести т = 0. Сега, за да се определи траекторията на точки: S = S (т) използване на дължината на дъгата от формула крива: или, предвид факта, че диференциация се извършва във времето, може да бъде презаписано, както следва. Знакът "+" се взема в случаите, когато се движи точка в положителна посока с препратка криволинейни координират с.
Какво е връзката между радиус вектора на движеща се точка и вектора на скоростта на този етап? Както е насочен вектор криволинейна скорост на движението на точка спрямо траекторията?
Ние се разлага на радиус вектора на декартова координатна система единичен вектор :. Сега ние се диференцират в уравнението по отношение на времето. Резултатът е скорост разлагане на векторите на дялове. , разширение може да бъде представена както следва :. къде. , - издатък на вектора на скоростта на координатните оси. По този начин издатините на фиксирана скорост Декартова координатна оси са равни на първа производно по отношение на времето на съответните координати на движещата се точка.
В вектор: За да се изчисли точно скоростта на точката, в даден момент, трябва да отиде във формулата на лимит периода от време, клони към нула, това е :. Това ограничение е първи път производно на вектора на вектора на радиус на момент от време. Както може да се види от тези формули, вектора на скоростта се отнася по допирателната към траекторията на движението му в посока.
Когато координира: Намираме таксовата единица, знаейки своята проекция :. За да се определи посоката на посоката уюта на скорост вектор работа:
. . . В резултат на това, ние все още prizhzhem до заключението, че вектора на скоростта е насочена по допирателната към траекторията.
С естествен :. ние знаем, че. Векторът е единичен вектор допирателна към пътя (неговата единичен вектор), насочена към възходящ криволинейна координира с. Обозначаващ първоначалния запис единица допирателна вектор като формула :. умножаване на лявата и дясната страна на уравнението на вектора на единица. , Препишете експресията както следва :. По този начин, се вижда, че скоростта вектор насочени тангенциално до точката на траектория.
Стойността се определя от големината и посоката на скоростта в момента на метод на координиране на задачи за движение?
. . По този начин издатините на фиксирана скорост Декартова координатна оси са равни на първа производно по време на съответните координати на движещата се точка. От уравненията това следва, че точката за скорост проекция върху координатната ос са проекциите на скоростта на този етап на една и съща ос. Познаването на проекцията на вектора на скоростта на точката, намери модул :.
За да се определи посоката на посоката уюта на скорост вектор работа:
Какво е връзката между радиус вектора на движеща се точка и вектора ускорение на точка? Както е насочена, за ускоряване вектора на движението на извитата точка по отношение на траекторията, лежи в равнина?
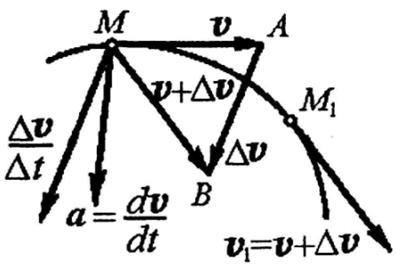
Сега се установи позицията вектор спрямо пътя. Имайте предвид, че триъгълник самолет MAV образувана вектори. и. когато се върти около вектора. т.е. около допирателната към траекторията в точката, F, и това отнема определен лимит в крайно положение. Това ограничение се нарича позиция MAP равнина допирателна равнина в точка М път. Средна вектор ускорение се отнася по същия начин, както. т.е. в вдлъбнатината на кривата, и през цялото време да е в равнината на MAB на триъгълник. Ограничаване вектор във вектор. който се намира в позиция ограничаване на триъгълника МАВ т.е. в допирателна равнина на траекторията на точка М. Така, векторът на пълна точка ускорение се намира в допирателна равнина на траекторията на М е насочена към вдлъбнатината на траекторията.