Личен сайт - числен кръг
числен кръг
Числен кръг - това е единица кръга, чиито точки отговарят на някои реални числа.
кръга на единица е кръг с радиус 1.
Общ изглед цифров обиколка.
1) радиус му се приема единицата.
2) хоризонтални и вертикални диаметри на разделена цифров кръг на четири четвърти (виж фигурата). Те са посочени съответно като първо, второ, трето и четвърто тримесечие.
3) Хоризонтална диаметър, определен AC и А - е най-дясната точка.
Означаваме вертикален диаметър BD, и В - е крайно горната точка.
Съответно:
Първа четвърт - тази дъга AB
второ тримесечие - дъга BC
трето тримесечие - дъга CD
четвърто тримесечие - дъга DA
4) Отправна точка цифров обиколка - точка А.
Четене на цифровата кръга може да се извършва както по часовниковата стрелка и обратно на часовниковата стрелка.
Преброяване от точка А обратно на часовниковата стрелка, наречено положителна посока.
Преброяване от точка А по часовниковата стрелка се нарича отрицателна посока.

Център радиус числен кръг отговаря на произхода (0).
Хоризонтална диаметър съответства на оста х. вертикална - ос у.
Изходните точка А цифров периферно разположен на х-ос и има координати (1, 0).
Имената и местоположението на основните моменти от реалния кръга:

Как да си спомня имената на цифров кръг.
Има няколко прости правила, които ще ви помогнат лесно да си спомня имената на главния цифров кръг.
Преди да започнете, ние си спомняме, като се брои в положителна посока, това е, от A (2π) обратно на часовниковата стрелка.
1) Да започнем с екстремните точки на координатните оси.
Отправна точка - е 2π (най-дясната точка на оста х е равно на 1.).
Както знаете, 2π - е дължината на окръжността. Следователно, половината от обиколката - на 1π или π. х ос разделя обиколката на само половината. Съответно, най-лявата точка на оста х. е равно на 1, наречен π.
Най-горната точка на оста у. равно на 1, разделя горната половина полукръг. Така че, ако полукръг - е пи, а след това половината от полукръг - е π / 2.
В същото време π / 2 - това е една четвърт кръг. Разчитаме на три четвърти от първо до трето - и се стигне до най-дълбоката точка на оста у. равна на 1. Но ако тя включва три четвърти - откъдето идва и името 3π / 2.

2) Сега е ред на другите точки. Забележка: Всички конфликтните точки имат една и съща числителя - и това е противоположната точка и спрямо у ос. и по отношение на централната ос, и х. Това ще ни помогне да се знае, техните стойности точкови без угояване.
Необходимо е да се помни, само стойността на първите точки тримесечие: π / 6, π / 4 и π / 3. И тогава ние "вижда" някои модели:
- По отношение на точките за ордината през второто тримесечие, срещу първите точки тримесечие, номерата в числителите 1 по-долу стойности на знаменателите. Например, да вземе точка π / 6. Неговата срещу точка по отношение на оста у, също има 6 в знаменателя и в числителя 5 (1 по-малко). Това е името на тази точка: 5π / 6. Точката срещу π / 4 също има 4 в знаменателя и в числителя на 3 (по-малко от 1 4) - т.е. точка 3π / 4.
В точка срещу П / 3, също има 3 в знаменателя и в числителя е по-малко от 1: 2π / 3.
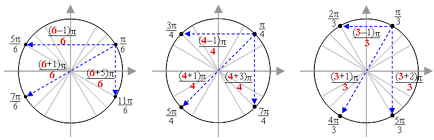
Точката срещу точката на π / 4 също има 4 в знаменателя и в броя на числител голямо от 1: 5π / 4.
Точката срещу точката на π / 3, също има 3 в знаменателя и в броя на числител голямо от 1: 4π / 3.
- В сравнение с оста х (четвъртото тримесечие) случаят е по-сложно. Тук е необходимо да се добави стойността на знаменателя на числото, което е една по-малко от - и тази сума ще бъде равна на цифровата част на числителя на обратното. Започваме отново с π / 6. Добавяне на стойността на знаменателя равна на 6, с номер, който е един по-малко от това число - т.е. 5. получаване: 6 + 5 = 11. Следователно, това обратното по отношение на точката на х-ос ще бъде 6 в знаменателя и в числителя на 11 - т.е. 11π / 6.
π / 4 точка. Ние увеличи стойността на знаменател на броя по-малък от 1: 4 + 3 = 7. Следователно, това обратното по отношение на точката на х-оста е 4 в знаменателя, числителя и 7 - т.е. 7π / 4.
π / 3 точка. В знаменател е 3. Ние добави към елемент 3 на минимален брой - т.е. получаване 2. 5. Следователно, неговата противоположност точка има числител 5 - и тази точка 5π / 3.
3) Друг модел за средата на четвъртата точки. Ясно е, че им знаменател е 4. Обърнете внимание на числителите. В числителя на средата на първото тримесечие - по 1 пени (но едно не е прието да се напише). В числителя на средата на второто тримесечие - е 3π. В числителя на средата на третата четвърт - на 5π. В числителя на средата на четвъртото тримесечие - с 7π. Оказва се, че в числителите в средата на четвъртата - първите четири нечетни числа във възходящ ред:
(1) π, 3π, 5π, 7π.
Също така е много лесно. От средата на всички квартали са в знаменателя на 4, което вече знаем пълните им имена: пи / 4, 3π / 4, 5π / 4, 7π / 4.
Характеристики на цифровата кръг. Едно сравнение с броя линия.
Както знаете, по редица линия, всяка точка съответства на уникален номер. Например, ако точка А по линията е равно на 3, не може да бъде равен на всеки друг номер.
От броя на кръга е различно, защото това е един кръг. Така например, от точка А до кръга дойде на точка M, можем да го направим като права линия (само след преминаване на дъгата), но можете да обикалят целия кръг, а след това стигна до точка М. Заключение:
Нека точка M е равна на някои брой т. Както е известно, обиколката е равна на 2p. Така че, кръг точка Т може да се запише по два начина: или т т + 2π. Тази равностойност.
Това означава, че т = т + 2π. Единствената разлика е, че в първия случай, вие сте попаднали на точка M наведнъж, без да прави кръг, и във втория случай сте направили кръг, но в крайна сметка се оказа в същата точка М. Тези кръгове могат да се направят две, и три, и двеста , Ако ние означаваме броя на обиколки с буквата к. получаваме нов израз:
т = т + 2πk.
Ако точка М е броят на цифров обиколка т, то е равно на броя и вида Т + 2πk. където к - всяко число: