Махало, и примери на формула

Pendulum - това е точката на материал. суспендира в дългосрочен безтегловност неудължаващ нишки (Фигура 1).

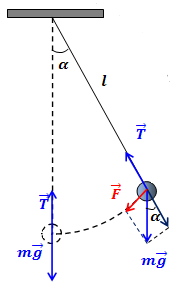
Фиг.1. махало

Pendulum - система модел се колебае. Свободно люлеене на махалото в математически малки деформации на ъгли са описани от хармонични трептения.

В състояние на равновесие на силата на гравитацията и силата на баланс еластичност нишки помежду си и материалната точка е в покой. В случай на материална точка от равновесното положение на малък ъгъл спрямо тялото ще действа възвратна сила, която е тангенциална компонент на силата на тежестта:

Тази сила се съобщава материал точка тангенциално ускорение насочени по допирателна към траекторията. и материална точка започва да се премести в позицията на равновесие с увеличаване на скоростта. Както приближава позицията равновесие на възвратната сила, и следователно намаляване на тангенциален точка ускорение. По време на преминаване, тангенциална равновесие ускорение ъгъл позиция на отклонение е нула, и скоростта на материал, а максимум. Освен материална точка преминава равновесното положение по инерция и се движи в посока, противоположна на силата намалява скоростта. В екстремна ситуация материалната точка спира и след това започва да се движи в обратна посока.

Периодът на колебание на махалото математически

Периодът на колебание на математически махалото не зависи от масата на товара и амплитудата на колебание.

Примери за решаване на проблеми

Махало с дължина 1 m варира с амплитуда от 1 см. От известно време ще бъде по пътя на 1 см, ако в първоначалното Време на махалото преминава равновесното положение? Колко време ще мине махало: а) за първата половина на тази пътека; б) През втората половина на този начин?

Периодът на колебание на математически махалото се определя по формулата:

Математически махало се колебае. така че изместването на материална точка, зависи от времето хармонично:

От първоначално махалото преминава равновесното положение, началната фаза на колебание е нула.

Пътят на 1 см, т.е. в този случай, равна на амплитудата на трептенията, махалото ще се проведе в една четвърт период, т.е. за 0.5 секунди.

а) В този случай, офсет:

така че ние може да пише:

б) Ако да премине през целия път, на равно амплитуда, махало харчи 0,5 секунди, и преминаването на първата половина - до 0,17, през втората половина от пътя на махалото ще похарчи:

Периодът на трептене на махалото 2; на прохода, на равно амплитуда, махалото ще похарчи 0.5; а) за първата половина на този път тя ще се 0,17 секунди; б) през втората половина от пътя - от 0.33.