Най-голямата и най-малката стойност на функцията на интервала

Да приемем, че функция у = F (х) е непрекъсната върху интервала [а, Ь]. Както е известно, функция за този интервал достига максимални и минимални стойности. Тези функции могат да се стойности или вътрешната точка на интервала [а, б], или на границата на сегмента.

За намиране на максималните и минималните стойности на функцията в интервала [а, Ь] е необходимо:

1) намерите критичен обхвата функция точка (А, В);

2) изчисляване на стойностите на функцията намерени в критичните точки;

3) изчисляване на стойностите на функцията на крайните точки, т.е. при х = а и х = В;

4) на всички изчислените стойности на функцията за избор на най-голямата и най-малката.

Пример. Намерете най-максимални и минимални стойности на функцията

Ние намираме най-критични точки:

Тези точки се намират в интервала [0; 3]; у (1) = - 3; у (2) = - 4; Y (0) = - 8; у (3) = 1;

в точката х = 3 и х = 0.

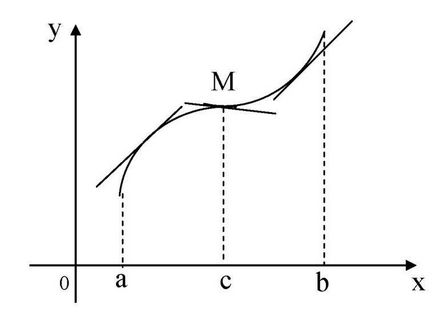
разполага изследвания на изпъкналост и инфлексна точка.

функция у = F В (х) се нарича vypukloyvverh интервала (а, Ь). ако неговата графика лежи под допирателната изготвен във всяка точка на интервала, и се нарича изпъкнала надолу (вдлъбната). ако нейната графика е над допирателната.

Точката в прехода през която издатина се заменя вдлъбнатина, или обратно, се нарича инфлексна точка.

Алгоритъм изследвания на изпъкналост и инфлексна точка:

1. Naydemi критичните точки на втория вид, т.е. точката, където второто производно е равно на нула или не съществува.

2. Нанесете критична точка на брой линия, я разделя на интервали от време. Намерете знака на втората производна на всеки интервал; ако функцията е вдлъбната, ако функцията е изпъкнала надолу.

3. При преминаване през критичната точка от втория вид ще се промени знак и в този момент втората производна е равна на нула, този момент - абсцисата на инфлексна точка. Намери своя ордината.

Асимптота на функциите на графиката. Едно проучване върху функцията на асимптотата.

Определение. Асимптота на графиката на функция е права линия. с имота, че разстоянието от всяка една точка в програмата за тази линия клони към нула с точката за отстраняване на графиката от произхода.

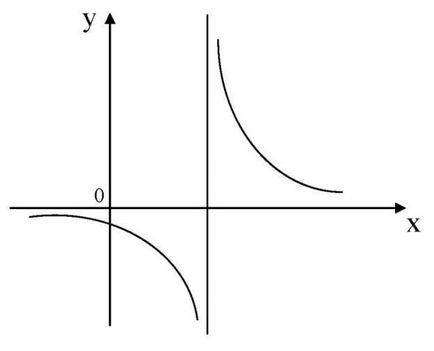
Има три вида асимптоти: вертикални, хоризонтални и наклонени.

Определение. Директен nazyvaetsyavertikalnoy асимптота на графиката на у = е (х). ако поне един от ограничения функцията едностранно в този момент е равна на безкрайност, т.е.

където - точката на прекъсване, а след това estne принадлежи на домейна.

х = 2 - точка почивка.

Определение. Директен у = А графика се нарича хоризонтална асимптота на функция у = F (х), ако