Ойлер графики - studopediya
Известният Ойлер проблем на Кьонигсберг мостове, съчленен езика на графики в 1736 е довела до математическа теория на графите. Тази игра проблем, същността на която е, както следва: в град Кьонигсберг на река Прегел, има два острова, които са свързани помежду си и по бреговете на седем мостове, както е показано на Fig.34. Разхождайки се из града, а от движението от всяка точка, която искате да мине през всеки мост точно веднъж и да се върнете към началната точка.
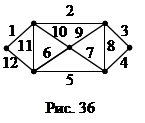
За всеки връх от сушата и всеки мост - ръба. Тогава "плана град" ще се появи, както е показано на фигура 35. И сега проблемът може да бъде преформулиран за графики: намерите в свързан граф затворена верига, която минава през всеки един от ръбовете му, или, както се казва, се отнася до всички краища на графиката. Такава верига се нарича Ойлер верига или Ойлеров цикъл. и графики, в които съществува такава верига, наречени Ойлер графики. Очевидно е, че графиката е показано на фигура 35, Ойлер не е така. Графиката на фигура 36 - Euler и съответния Ойлер верига - последователност на ръбове (1,2, ¼, 12).
Теорема 3.13.1. Connected графика е Ойлеров единствено и само ако всеки връх има дори степен.
Доказателство: (а) Да приемем, че графиката е Ойлеров и С - цикъл Ойлер. След това, преминавайки на ръба с всеки един от върховете, ние го увеличи с 2 градуса, а защото всеки край на графиката се намира в C точно веднъж, степента на всеки връх ще бъде четен брой.
(В) Сега нека всеки връх има дори степен, т.е. ° (VI) ³2 за произволен брой връх аз. Затова графиката още няма висящи върхове, и това не е дърво. Ето защо, в колоната трябва да бъде поне един цикъл, дори ако то C1. Разглеждане на графика G1 = G \ С1. Всеки връх на G1 трябва да има дори и степен, тъй като всички върхове имат степен C1 2. Въпреки това е възможно, че G1 - изключен графика. Ако G1 се състои от изолирани върхове, т.е. ° (VI) = 0 за всички аз. цикъла С1 - и теоремата Ойлер оказа, ако това не е така, тогава всеки компонент G1 - е свързан граф с върха на дори степен, и всеки компонент има най-малко един цикъл. (Може да се предположи, че G1 състои от изолирани върхове и един свързан компонент). Нека този цикъл C2 1, C2 2, ¼, C2k. Помислете сега графика G2 = G1 \ C2. където C2 =. Точно както преди степента на всеки връх на G2 на графика - равна или нула. Ако G2 се състои от изолирани върхове, след това графиката има цикъл Ойлер, който може да се получи както следва: отиде С1 цикъл ребра, докато отговарят на върха, принадлежащи към всеки компонент на G1 на графика (тези върхове са длъжни да има, защото . оригиналния графиката е свързан). След това проверете цикъл на компонентите, а след това продължи да се движи по В1 ръбове. до следващите компоненти връх срещнат и да ходят на ребро цикъл на този компонент, а след това отново да преминем към следващите елементи C1 и т.н. Ние обикалят всички краища на графиката само веднъж и да се върнете към началния връх. Ако G2 има не-изолиран отгоре, тогава те формират свързани компоненти, всеки от които има най-малко един цикъл С3 1, С3 2, ¼, C3k. След това разглеждане на графика G3 = G2 \ C3. където C3 =. Ако G3 се състои от изолирани върхове, а след това на теоремата е доказано и може да бъде определен цикъл Ойлер процедурата. В противен случай, премахване на всички цикли G3 и действа така, до тогава, докато графика, състояща се само от изолирани върхове.
Следствие 1: семейство ребра Ойлер графика може да бъде разделен на несвързани цикли в ребрата.
Следствие 2: Ойлер всеки връх на графиката се съдържа в поне един цикъл.
Теорема 3.13.2. Във всеки свързан граф с нечетни 2k върховете на семейството на к вериги (не пресичащи ребрата), които заедно покриват всички краища на графиката.
Доказателство: Ще означаваме нечетни върхове: А1. А2. ¼, Ак. B1. В2. ¼, Бк - във всички 2k върхове. Добавяне на броя к на ребра (А1, В1), (А2, В2), ¼, (Ak, Bk). Сега всички върхове имат дори градуса, а има и Ойлеров цикъл. Премахване на писмени к ребра, ние се прекъсне цикъла к вериги, съдържащи всички краища на първоначалната графиката.
Следствие. Ърл е polueylerovym единствено и само ако тя има точно два върха на странно степен. Очевидно една от тези върхове ще започне да отвори верига графиката Ойлер, а другият - най-доброто.
Помислете за строителство алгоритъм Фльори Ойлер верига в Eulerian графика.
Нека G - Euler графика, а след това по-долу процедура, винаги е възможно, и води до Ойлер графика верига Г. Идвайки от произволен връх, отидете по ръбовете на произволен начин, спазвайки само на следните правила: 1), за да изтриете краищата, тъй като те преминават и да изтриете също изолирани върхове, който по този начин се образуват; 2) на всеки етап от случва през моста само когато няма други възможности.