Параметрично зададени функции
Връзката между аргумента и функцията може да се запише по отношение на допълнителната променлива, наречени параметри, т.е., на система, в която предписаната зависимостта на аргумента на параметъра и зависимостта на функцията на същите параметри:
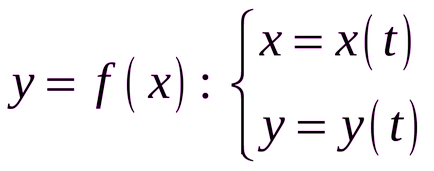

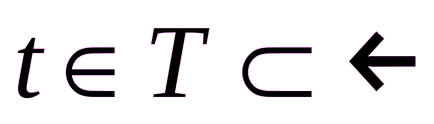
В този случай nazyvaetsyafunktsiey функция дефинирана по параметри.
Графиката на функция у = F (х) е набор от всички точки, чиито абсцисата принадлежи към областта на функцията, и стойностите на съгласува са равни на съответната функция.
С други думи, графиката на функция у = F (х) - е множеството от всички точки в равнината с координати X, Y отговарят връзката у = е (х).
Основен елемент на поведението на функцията
функция у = F В (х) е дори ако тя отговаря на следните две условия:
1. Област на определянето на тази функция трябва да бъде симетричен около точката О. Това означава, че ако една точка принадлежи към областта на функцията, съответната буква -а също трябва да принадлежат към областта на дадена функция.
2. Стойността на функцията на точка х принадлежност домейн на функцията е равна на стойността на функцията на точка за -X. Това означава, че за всяка точка х в областта на функцията трябва да отговаря на следното уравнение е (х) = F (-x).
Ако се направи графика на още по функция, тя ще бъде симетричен по отношение на оста у.
Например, тригонометрична функция Y = COS (х) е дори
у = функция е (х) се нарича странно, ако отговаря на следните две условия:
1. Област на определянето на тази функция трябва да бъде симетричен около точката О. Това означава, че ако една точка принадлежи към областта на функцията, съответната буква -а също трябва да принадлежат към областта на дадена функция.
2. За всяка точка х в областта на функцията трябва да отговаря на следното уравнение е (х) = -f (х).
Графиката на нечетен функция е симетрична по отношение на точка O - произход.
Например, тригонометрична функция у = грях (х), у = TG (х), Y = CTG (х) е нечетен.
функция у = F В (х) е периодично, ако съществува някакъв брой Т! = 0 (нарича период на функция у = F (х)), така че за всяка стойност на X в областта за определяне на функцията, броят х + T и х T също принадлежат към областта на функцията и следното равенство F (х) = F (х + T) = F (XT).
Трябва да се разбере, че ако Т - период на функцията, броят на к * T, където к е цяло число, различно от нула, ще бъде също период на функцията. Въз основа на изложеното по-горе, ние откриваме, че всяка периодична функция има безкраен брой периоди. Най-често, разговорът е за най-малките елементи период.
Тригонометрична функция грях (х) и COS (X) са периодични с период равна на най-ниската 2 * П.
Тригонометрични функции TG (X) и CTG (X) са периодични с период, равен на най-малкия П.
функция у = F на (X), определена на набор X. наречена ограничена по-горе, ако множество стойности ограничава горната си. С други думи, на функцията F е ограничена по-горе, ако съществува константа М, че неравенството притежава всеки.
функция у = F на (X), определена на набор X се нарича ограничена долу, ако множеството от нейните стойности се ограничава от по-долу, това е, ако съществува постоянна М че kazhdogovypolnyaetsya неравенството. Например, това са експоненциални функции, funktsiiy = x2n, у = x.
F функцията (х), определена на набор X, наречен ограничен. ако множеството от стойностите му са ограничени както от горе и от долу. Примери за функции, които са ограничени върху реалната линия, е функция у = грях х, у = COS X, Y = ARccOS X, Y = arcsin X, Y = arctg X, Y = arcctg х.
а) ако за всички х от някои набор от неравенството х е (х)> М, и г (х)
б) ако за всички х от някои набор от неравенството х е (х) M и г (х) M. където М - число, след определен Х към уравнение е (х) = грам (х) е еквивалентна на системата
Ако функцията се увеличава или намалява по някакъв интервал, а след това той се нарича монотонно на този интервал.
Забележете, че ако е - монотонна функция на интервал г (е (х)), тогава F уравнение (х) = конст може да има повече от един корен в този интервал.
В действителност, ако x1
Ние списък на свойствата на монотонни функции (предполага се, че всички функции, определени в определен интервал D).
Сумата от няколко увеличават функции е нарастваща функция.
Произведение неотрицателно нарастваща функция е нарастваща функция.
Ако функция F се увеличава, след това функции CF (C> 0) и е + C също се увеличава, и CF на функция (в <0) убывает. Здесь c – некоторая константа.
Ако F увеличава и запазва своя знак, функцията 1 / F намалява.
Ако функция F се увеличава и не е отрицателен, когато също се увеличава.
Ако F увеличава и п - нечетно число, а след това Fn също се увеличава.
Състав г (е (х)) увеличаване функции е и ж също се увеличава.
Основни елементарни функции