Предизвикателства за изчисляване на повърхността на различни видове polyhedra

Предизвикателства за изчисляване на повърхността на различни видове polyhedra

Създаване 8_1. Намери полихедронов повърхностна площ е показано на фигурата (всички двустенни ъгли са прави ъгли).

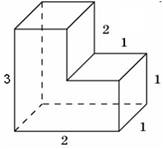
Повърхностната площ на многостен може да бъде изчислена като сумата от площите на неговите страни. Където областта на предните и задните страни са

и цялата площ на повърхността е

Създаване 8_2. Намери полихедронов повърхностна площ е показано на фигурата (всички двустенни ъгли са прави ъгли).

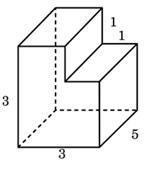
Намираме повърхностната площ като площта на правоъгълен паралелепипед със страни 3, 3, 5 и изважда 1x1 квадратен две лица на правоъгълен паралелепипед със страни 1, 1 и 3 (вж. Фигура).

Повърхностната площ на голям паралелепипед е

Square е изправен пред две 1x1 малък паралелепипед, са:

и площта на фигурата

Създаване 8_3. Намери полихедронов повърхностна площ е показано на фигурата (всички двустенни ъгли са прави ъгли).

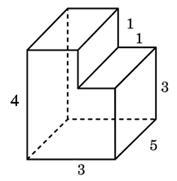
Фигурата показва, че формите на повърхност площ ще бъдат по-малки от областта на правоъгълен паралелепипед със страни 3, 4 и 5 в областта на двете квадрати с размер 1x1, имаме:

Създаване 8_4. Намери полихедронов повърхностна площ е показано на фигурата (всички двустенни ъгли са прави ъгли).

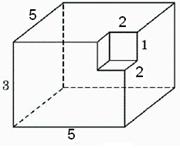
Тя може да се види, че площта на фигурата ще бъде точно същата като площта на правоъгълен паралелепипед със страни 5, 3 и 5 и е равна на

Забележка. Не бъркайте изчисляването на обема на фигурата и нейната повърхност!

Създаване 8_5. Намери полихедронов повърхностна площ е показано на фигурата (всички двустенни ъгли са прави ъгли).

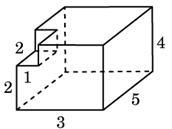
Повърхностната площ на тази фигура е площта на правоъгълен паралелепипед със страни 3, 4 и 5, и е равна на

Забележка. Не бъркайте изчисляването на обема на фигурата и нейната повърхност!

Създаване 8_6. Намери полихедронов повърхностна площ е показано на фигурата (всички двустенни ъгли са прави ъгли).

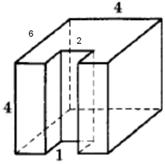
Повърхностната площ на тази фигура може да се изчисли като площта на правоъгълен паралелепипед с страни на 4, 4 и 6 плюс две лица 1x4 област 4 (вж. фигура) и минус две лица 2x1 квадрат (те се изважда от база). По този начин, площта на фигурата е

Създаване 8_7. Намери полихедронов повърхностна площ е показано на фигурата (всички двустенни ъгли са прави ъгли).

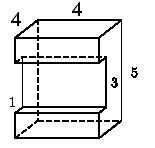
Квадрати на долните и горните лица на равна площ от страничните стени могат да бъдат изчислени като площта на съответно на предните и задните ръбове, и по-необходимо да се разгледат две области вътре в горните и долните лица. Така цялата повърхност на фигурата е

Създаване 8_8. Намери полихедронов повърхностна площ е показано на фигурата (всички двустенни ъгли са прави ъгли).

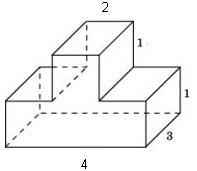
Формата на повърхност площ могат да бъдат изчислени като площта на правоъгълен паралелепипед със страни от 4, 3 и 2, минус четири квадратен странични квадрати 1x1. В момента има:

Създаване 8_9. Намери полихедронов повърхностна площ е показано на фигурата (всички двустенни ъгли са прави ъгли).

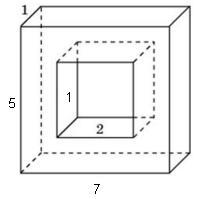
Цифрата показва правоъгълен паралелепипед с отрязани. Повърхностната площ на фигурата ще бъде равна на цялата повърхност на паралелепипед със страни 5, 7 и 1 минус два челната вдлъбнатина площ областта на 2x1 = 2 и плюс четири вътрешни страни на зоната на предварителния изрез размери 1x1 и 2х1. Така цялата повърхност на многостен е равно на

Създаване 8_10. Намери полихедронов повърхностна площ е показано на фигурата (всички двустенни ъгли са прави ъгли).

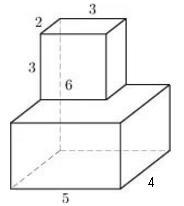
Повърхностната площ на многостен може да се намери като сума от квадратите на две правоъгълен паралелепипед със страни 5, 4, 3, 3, 2, 3 минус две долни паралелепипед квадратна основа площ на 2x3 (две области, тъй като се счита, в две големи и малки паралелепипеди) , По този начин, ние получаваме:

Създаване 8_11. Намери полихедронов повърхностна площ е показано на фигурата, всички двустенен ъгъл прав.

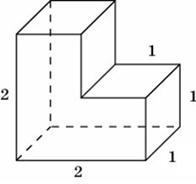
Намираме повърхност на фигурата като площта на правоъгълен паралелепипед със страни 2, 2, 1, и изважда двете страни на квадрат 1x1 в предна равнини (предни и задни), ние получаваме:

Създаване 8_12. Виж повърхностна площ на кръста е показано на фигурата и се състои от единични кубчета пространствен.

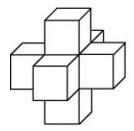
Площта на повърхността на фигурата може да се намери като сумата от площите на 6 кубчета минус площта на куб (един вътре и тези лица не са включени в площта) на повърхността, получаваме:

Създаване 8_13. Намери полихедронов повърхностна площ е показано на фигурата (всички двустенни ъгли са прави ъгли).

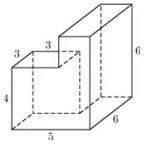
Ние считаме, че площта на полихедронов като сумата от площите на големи (6h6h2) и малки (3h3h4) Кубоидите събиране и изваждане на два пъти площта на лицата за контакт на паралелепипеди, които е с размер 3x4, получаваме:

Създаване 8_14. Намери полихедронов повърхностна площ е показано на фигурата (всички двустенни ъгли са прави ъгли).

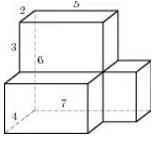
Повърхностната площ на многостен може да се намери като сума от площите на всяка от трите измерения 2h5h6 паралелепипеди, и 2h5h3 2h3h2 минус два пъти площта на контакт на тези паралелепипеди, т.е. минус два пъти площта на двете страни на размери 3x5 и 2x3 съответно. Резултатът е с площ от фигурата:

Създаване 8_15. Чрез средната линия триъгълна призма база равнина поддържана успоредно на страничния ръб. Виж областта на страничната повърхност на призмата ако повърхност на страничната е отрязана с триъгълна призма 37.

Тъй като равнината на напречното сечение изтегля през средната линия, тя се разделя на половина на страничната равнина. Следователно, по-голямата повърхност на страничната на призмата 2 пъти по страничната повърхност е малък и призмата 74.