продукт точка на два вектора и неговите свойства

Определение. Скаларно произведение на два вектора

ие число, равно на продукта от модули векториикосинуса на ъгъла между тях.

В скаларен продукт на два вектора

ипредставляват, или.

Така че, по дефиниция,

,

където

- ъгълът между векторитече.

Ако най-малко един от векторите е нула, тогава ъгълът не е определено и скаларен продукт по дефиниция се счита за нула.

Тъй формула

скаларното продукт с формула могат да бъдат написани по следния начин:

.

По този начин, скаларен продукт на два вектора е равна на произведението на модула на векторите на проекция на втори вектор на първия.

Скаларни продукт има следните свойства:

1.Skalyarnoe продукт е комутативен, т.е. за всички вектори

. (2.14)

2, т.е. за произволен вектор на своята скаларна квадратен е равна на квадрата на единичен вектор. тук

. (2.15)

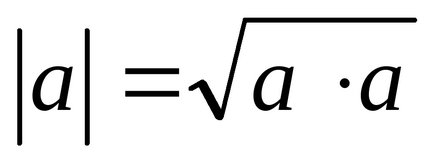
3. скаларен продукт е равно на нула, ако и само ако фактори са ортогонални, или най-малко един от тях е нула.

4. скаларен продукт е асоциативен по отношение на скаларна фактор, т.е.. (2.16)

5. скаларно произведение разпределителни по отношение допълнение, това е, за всеки три вектори

имаме равенство

.

6. ортонормирани базисни вектори удовлетворяват зависимостите:

,

.

Нека сега разгледаме два вектора

и, която определя координатите в декартова координатна система:;,

След това, използвайки горните свойства на скаларен продукт, получаваме

, скаларен продукт на два вектора в ортонормирана основа е сумата от произведенията на техните координати.

, вектор модул е ​​корен квадратен от сумата от квадратите на координатите.

Косинуса на ъгъла между двата вектора

.

За да се получи основа на ортонормален:

и ортогоналността на два вектора става :.

Продуктът от вектор на два вектора, неговите свойства

Дефиниция 2.21. Вектор продукт на вектора

векторТова е вектор(Фигура 2.15.), В която: 1), дължината е числено равна на площта на успоредник конструирана на тези вектори.

2) векторът перпендикулярна на равнината, в която векторитеи, т.е.и;

3) на вектора

Той е насочен така, че да се включи най-краткия векторна вектораизвършва обратна на часовниковата стрелка, когато се гледа от края на вектора.

Vector продукт

иозначенили.

От определението следва, че свойства:

2) - на асоциативност на множителя на скаларна;

3) - разпределителни над допълнение;

4)

Това е колинеарни вектории.

За основния вектор продукт на векторите на единица

притежава такава таблица (Таблица 2.1).