Строителство на триъгълника на трите елемента

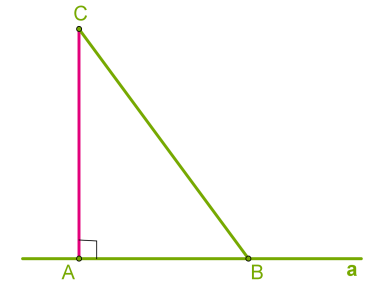
1, всички други сегменти, проведени от тази точка на линията, наречени наклонена ако точка \ (С \) към линия \ (а \) проведе перпендикулярна \ (Калифорния \).

2. перпендикулярен проведено от точката на права линия, е по-малък, отколкото който и да е склонен проведено от тази точка до тази линия, както и в правоъгълен триъгълник хипотенуза вече крак.

3. Дължината на перпендикуляра проведено от гледна точка на ред нарича разстоянието от тази точка на линията.

Разстоянието между успоредните линии

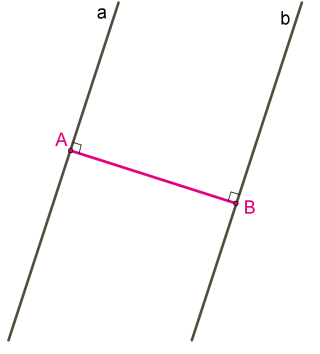
Всички точки на една от паралелни линии на еднакво разстояние от другата успоредна линия.

Следователно, разстоянието между две успоредни линии перпендикулярни определена дължина спадна от всяка точка взети по линия към друга линия.

Строителство на триъгълника на трите елемента

Темата на строежите са разгледани:

1. Как да се направи кръг с даден център и радиус.

2. Тъй като в този лъч от неговото създаване до отложат сегмент, равна на тази.
3. Как да се изгради под ъгъл, равен на този.
4. Как да се изгради ъглополовящата на ъгъла.
5. Как да се изгради една перпендикулярна линия.
6. Как да се изгради една средна точка.

Използването на разглеждания изграждането и елементите на данните, на триъгълника, можем да изградим един триъгълник е равен на настоящето.

Строителство на триъгълника на двете страни и ъгъла между тях.

Като се има предвид две сегмент \ (а \) и \ (б \), те са желани страните на триъгълника и ъгъла ∡ \ (1 \), равен на ъгъла между страните на триъгълника. Необходимо е да се изгради един триъгълник с елементи, равни на сегментите от данни и ъгъла.

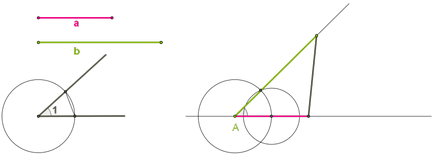
1. Начертайте права.

2. В права линия от избраната точка \ (А \) за забавяне интервал равен на този сегмент \ (а \).

3. Изграждане на ъгъл, равен на този ∡ \ (1 \) (връх ъгъл \ (А \), от едната страна на ъгъла на линията).

4. От другата страна на ъгъла за забавяне интервал равен на този сегмент \ (б \).

5. Свържете краищата на сегментите.

Според основата на равенството на триъгълници от двете страни и ъгълът между тях, триъгълник е построена с всички триъгълници, които имат тези елементи.

Строителство на триъгълника до рамо и две съседни, за да си ъгли.

Предвид интервал \ (а \) и два ъгъла ∡ \ (1 \) и ∡ \ (2 \) равен на ъглите на триъгълника, съседни на тази страна. Необходимо е да се конструира триъгълник с елементи, равни на даден сегмент и ъглите.

1. Начертайте права.

2. В права линия от избраната точка \ (А \) за забавяне интервал равен на този сегмент \ (а \), а другият край на сегмента марка \ (B \) на.

3. Изграждане на ъгъл, равен на този ∡ \ (1 \) (връх ъгъл \ (А \), от едната страна на ъгъла на линията).

4. Конструкция на ъгъл, равен на този ∡ \ (2 \) (връх ъгъл \ (B \), от едната страна на ъгъла на линията).

5. пресечната точка на други странични ъгли е третият връх на желания триъгълник.

Според функция на равенство на триъгълника до рамо и две съседни, за да му ъгъла, на триъгълника е построена с всички триъгълници, които имат тези елементи.

Предвид три сегмента: \ (а \) \ (б \) и \ (в \), равна на страната на желания триъгълник. Необходимо е да се изгради триъгълник със страни са равни сегменти на данни.

В този случай, преди да създадете необходимо да се провери дали неравенството на триъгълника се изпълнява (дължината на всяка секция е по-малка от сумата от дължините на другите два сегмента), и тези сегменти могат да бъдат страни на триъгълник.

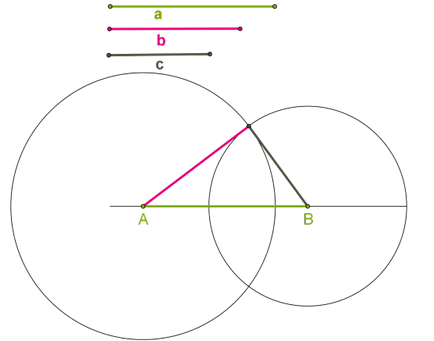
1. Начертайте права.

2. В права линия от избраната точка \ (А \) за забавяне интервал равен на този сегмент \ (а \), а другият край на сегмента марка \ (B \) на.

3. Извършва окръжност с център \ (А \) и с радиус, равен на сегмент \ (б \).

4. Извършва окръжност с център \ (B \) и с радиус, равен на сегмент \ (в \).

5. точката на пресичане на кръгове е третият връх на желания триъгълник.

Според основата на равенството на триъгълници от три страни, триъгълник е построена с всички триъгълници, които имат отношение на данните.