Теория на графите основни дефиниции

Графика теория - клон на математиката, използвани в компютърните науки и програмиране, икономика, логистика, химия.

Какво е Ърл

Често, за да опише структурата на системите, използващи блок-схеми. Елементи, които те представляват кръгове, точки, площади и т.н., и връзки между елементи - .. Линии или стрели. В този случай, нито колко елементи са показани, нито дължината или формата на линиите не е важно - въпроси само кои елементи са свързани. Така че, Ърл - чифт формата (А, М), където А - ограничен набор от върха, и М - набор от ръбове - линии, свързващи някои от върховете.

Основни понятия от теория на графите

В насочено графика или диграфа (вж. Фигура долу), ориентирани ребро, наречени арки и са представени със стрелки. Дъгата може да бъде определена от наредена двойка върхове, които го свързва, - в началото и в края.

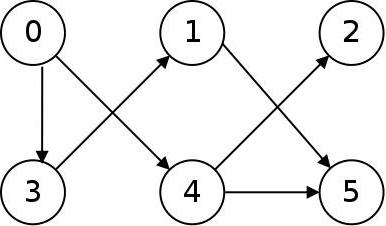
В ненасочена графика (вж. Фигура по-долу) са представени чрез линии без ръб ориентация. Съответно, двойката на върха, който свързва реброто е нарушено. И двете срещи са краища на ребрата.

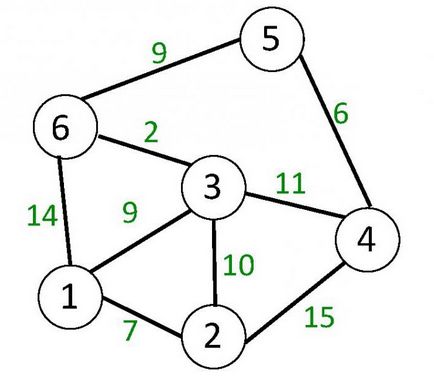
Ако върховете А - В краищата на ребрата (или в началото и края на дъгата) на графиката, тогава ние се каже, че върховете А и В са инцидент на този ръб (дъга), както и един ръб (дъга) е инцидент с върховете А и Б. Ако върховете А и В - краищата на ребрата, те са (а и б) казва, че е в непосредствена близост.

Най-често считат графики, чиито краища са един вид - са ориентирани или не.

Ако краищата имат една и съща началото и в края, те се наричат ​​множество ръбове, графика, в която те се намират, се нарича мултиграф.

Графика теория също използва термина "линия" - край става и настройка в една и съща върха. Графика, в който има една линия, наречени pseudographs.

Най-често срещаните неориентирани графа, че не разполагат с множество ръбове и без вериги. Тези графики се наричат ​​обикновени. Те не разполагат множество ръбове, така че можете да идентифицирате реброто и съответстващата двойка върхове.

Всеки връх на диграфа се характеризира с:

• Половин резултат. Това е броят на дъгите, произтичащи от него.
• Indegree. Това е броят на дъгите, които са включени в тази среща на върха.

Обобщете indegree диграфът, и сумата outdegree равен на общия брой на дъги.

В ненасочена графика, всеки връх има степен на връх. Така е броят на ръбове, които са инцидент до върха. Общата сума на степените на върховете е броят на ръбове, умножена по две: всеки ръб ще даде своя принос, който е равен на две.

Vertex с степен 0 се изолира.

Висящи връх е връх, със степен на един.

Графика теория нарича празен графика, в която няма ръбове. Пълен граф - това е един обикновен графика, в която всеки две съседни върхове.

Статистическа графика - графика, чиито върхове или ръбове (дъги), от които или и двете върхове и ръбове (дъги) веднага дължи някои номера. Те са наречени тежести. Вторият Фигурата показва ненасочена графика, чиито краища са претеглени.

Графики: изоморфизъм

изоморфизъм понятие се използва в областта на математиката. По-специално, графика теория определя: две графики U и V са изоморфни ако тези графики има Биекция между наборите от върховете: всеки 2 върховете U колона, свързана с предимство, ако и само ако свързани край в V графика същото върхове (което може да има друго име). Фигурата по-долу показва две изоморфни графика, в която върховете между боядисани в същия цвят в първата и във втората колона, има Биекция описано по-горе.

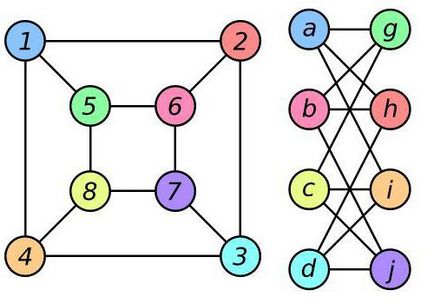
Пътища и цикли

Чрез в ненасочена или насочено графика е последователност от ръбове, където всеки следващ започва в горната част, която завършва предишния. Един прост начин - тази, в която всички върхове, с изключение може би на началото и края, а ребрата са различни. Един цикъл е път в диграфа, което съвпада с начало и край връх и която включва най-малко един кош. Цикъл на ненасочена графика е пътека, която съдържа най-малко три различни краища. Вторият фигурата е контур, например, пътя (3, 1), (6, 3), (1, 6).

Графика теория в програмирането се използва за изграждане на графиката-схеми на алгоритми.