Движение на заредена частица в магнитно и електрическо поле
Част 3: електричество и магнетизъм
Раздел 9 от магнетизма. Магнитното поле на електрическа енергия
9.6. Движение на заредена частица в магнитно и електрическо поле. сила на Лоренц
А проводник, през който протича ток е различен от сегашния диригент без това става въпрос методично придвижване на носители на заряд. Това предполага, че силата, която действа на тоководещи проводник поставен в магнитно поле се дължи на действието на силите на отделните движещи такси. И вече от действието на тези такси се предава проводник, чрез които те се движат. Този подход дава възможност да се определи силата, която действа върху отделна такса, която се движи в магнитно поле. Тя се нарича сила на Лоренц.
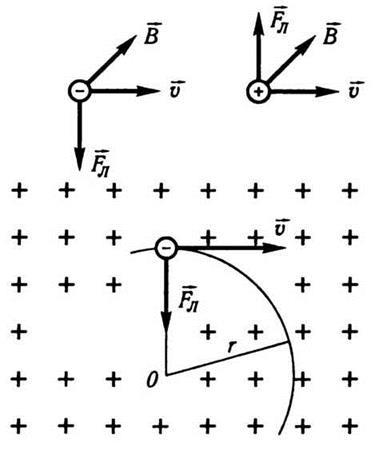
Да предположим, електрон със скорост. Той лети в постоянно магнитно поле на индукция B както е показано на фиг. 9.7. Линии на магнитната индукция и етикетирани кръст насочени от читателя перпендикулярно на равнината на фигурата. А движи заредена частица е електрически микроток. След това, за да се определи силата, с която магнитното поле действа на движещ се заряд д (д - електронен заряд), които можете да използвате закона на Ампер. Съгласно закона ампера да елемент ток л праволинейни постоянно магнитно поле с индукция действа със сила равна α IlBsin [формула (9.21)] (α - ъгъл между областта и ток). Нека движещ такса д във време тон се премества на разстояние л. Това е подобно на текущия елемент, чиято сила I =. Заместването този израз във формула (9.21), ние получаваме л Bsin α. Като се има предвид, че в този случай, грях α = л и л / т = υ. най-накрая получаваме израз за силата на Лоренц:
За да се определи посоката на силата на Лоренц може да се прилага като цяло остави ръка. Въпреки това, в този случай, на пръстите на ръцете трябва да не се поставят в посоката на движение на електрона, и срещу неговото движение, тъй като електронът е заредена отрицателно, а за посоката на посоката на тока взето положителни заряди. Използване на понятието вектор продукт, формула (9.26) може да се запише в тази форма:
Тогава (9.27) в същото време да се определи стойността и посоката на силата, действаща в магнитно поле на движещ се електрон. Посоката на силата, действаща в магнитното поле на положително заредени частици, съвпада с посоката на вектора на продукта, [], т.е.
Формули (9.27) и (9.28) могат да бъдат комбинирани
но трябва да се разбира от р алгебрични стойност на таксата, която се движи (р> 0 за положителни заряди и р 0 за отрицателно). Фиг. 9.7 показва относителните позиции на векторите L. За положителните и отрицателните заряди.
Тъй като сила на Лоренц L е винаги перпендикулярна на скоростта на заредената частица, той не извършва работата, а само се променя посоката на движение на заредена частица в магнитно поле. Като абсолютна стойност обвинен скоростта на частиците и кинетичната енергия, не са се променили. Лоренц сила е центростремителна сила и осигурява заредена частица, центростремителната ускорение е равна. където V - скорост на движение на електрона; R - радиусът на кривината на траекторията на електрони в магнитно поле. След това с помощта на векторите перпендикулярни аз. записвам
където Q - зареждане на частицата; m - неговата маса.
Формула (9.30) показва, че следователно траекторията на заредената частица, която влиза в постоянно магнитно поле (с = конст) под ъгъл спрямо линията на магнитната индукция и има същата кривина е кръг с радиус, като се излиза от уравнение (9,30) е равна на
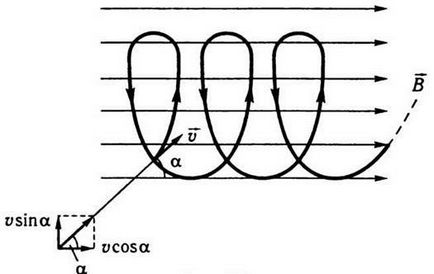
Ако пространството, където се движи заредена частица създава магнитно поле napryamlene под ъгъл алфа своята скорост, по-нататъшното движение на частиците може да се разглежда като геометричен сбор от две движения, които се случват в същото време, а именно, въртенето на окръжност със скорост υ α греха в равнина, перпендикулярно на линии, и се движат по протежение на областта с υ скорост защото α. Следователно, траекторията на частицата, в този случай е под формата на спирала, чиято ос е успоредна на посоката на вектора (фиг. 9.8).
Ефект на електрическото поле на движението на електрон или други заредени частици се различава значително от влиянието на магнитното поле. Електрическото поле променя кинетичната енергия на електрона, докато магнитното поле се променя само посоката, но не и неговата скорост. Движението на заредени частици като електроните в електрическо поле обикновено е подобен на движение на тялото в гравитационното поле: ако началната скорост на електрона е противоположна на посоката на силовите линии на хомогенна електрическо поле, силата, действаща върху него съвпада с посоката на скоростта - електрон движи rіvnopriskoreno. В обратна посока ще се движи скорост rіvnospovіlneno. Ако началната скорост на електрона е перпендикулярна на посоката на линиите на полето на електрическото поле хомогенна, електрона ще опише парабола.
В сила, упражнявана от униформа електрическото поле на електрона, който се влива в това перпендикулярно на линията на напрежение само при първоначалното време е центростремителна. Следователно, радиусът на закръгление R на електрона до началната точка на параболата може да бъде изчислено от съотношението
където E - електрическо поле; m - маса на електрона. По този начин, за електрони, които се отклоняват напречно електрическо поле, радиусът на кривината на пътя е пропорционална на квадрата на скоростта:
В общия случай, подвижен електрически заряд Q може да работят едновременно с индукция на магнитното поле и електрически интензивността на полето се характеризира. След това, резултантната сила. в качеството на заряда е равна на сумата от вектор сили е = Q. който работи на акция на електрическото поле и Лоренц сила L = Q [,]:
Този израз се нарича формула Лоренц. Според (9.31) при отклонение на електрон магнитно поле, радиусът на кривината на траекторията е пропорционална на скоростта. Тази функция се използва за измерване на скоростта на електроните по взаимно компенсиране на действието на електрическите и магнитните полета върху електрон движение.
Поставяне на плоски полюсите на електромагнит, така че линиите на магнитното поле са перпендикулярни на силовите линии на електрическото поле и потока на електрон преминава едновременно между полюсите на електромагнит и плоча равнина кондензатор, след регулиране на тока в електромагнита намотка (промяна на магнитната индукция поле), отклонението на електроните от линейна пътека, предизвикана от електрическо поле, могат да бъдат напълно компенсирани от една и съща стойност, но противоположна по посока на отклонението, причинени от магнитното поле. От формулите за радиусът на кривината на траекторията на електрони в напречна електрически (9.33) и магнитни (9.31) области може да се види, че отклонението може да бъде взаимно компенсира
или връзката
Тази формула позволява да се определи скоростта на заредени частици (електрони) измерване на електрически и магнитната индукция на полето, избрани така, че техните действия са взаимно шарнирно kompensuvalis. Ако след това премахване на електрическото поле и измерване на отклонение на електроните в магнитното поле, а след това най-R. E и B може да се определи конкретна заряда на електрона - съотношението на таксата за електрон към маса. Формулата за изчисляване на това съотношение може да бъде получено от (9,31) и (9,35):
Специфичната заряда на електрона за първи път е дефинирана от Джордж. Томсън. Въз основа на измерванията в електрически и магнитни полета, огъването на катодните лъчи, беше установено, че
Като се има предвид, че началното зареждане е = 1602 ∙ 10 - ПК 19, и като се знае д / м. ние откриваме, че електрон маса М = 9,109 ∙ 10 -31 кг.
Метод за определяне д / т, може да се използва при всички частици в потока имат една и съща скорост. Всички електрони, образуващи сноп, ускорено чрез същия потенциал разликата, която се прилага между катода, от която те се отделят и анода; Следователно разпръсне електрон скорости на потока е много малък.
Положителните йони се образуват чрез йонизация на газови молекули. Включени в различни места, различни йони преодоляване потенциална разлика, при което скоростта на различни йони различават един от друг. Следователно, методът, по който специфичното заряд на електрона, е определено, не се прилага към йони.
През 1907 г. Джордж. Томсън е разработила "метод за параболи", с които можете да се определи конкретна заряда на йоните.
. Извършване експеримент с химически чиста неон, и J. Thomson установено, че този газ образува парабола две съответстващи атомни маси 20 и 22. Опитите да се обясни този резултат води до предположението, че има два вида химически неделими неонови атоми (в съвременната терминология - две неон изотоп) , F. доказано това предположение на Aston, който подобрява метод за определяне на специфичния заряд на йона. Устройство с помощта на което може да се определи д / m на различни йони, F. Aston нарича маса спектрограф.