Ъглите, математика

Две прави линии ВА и BC (фиг. 13), се пресичат в една и съща точка В, точка Б е оформен в един ъгъл.

Определяне на ъгъла. Angle се нарича неопределен част на равнината, ограничена от две пресичащи се прави линии. Ъгълът е количество, което определя наклона на правата линия към друга.

Страни ugla.Peresekayuschiesya линии се наричат ​​страни на ъгъла.

Vertex на ъгъла. В точката на пресичане на две линии се нарича върха на ъгъла. Големината на ъгъла е независимо от дължината на страните, така ъгъл страна може да продължи неопределено време.

Името на ъгъла. а) Ъгли нарича писмото, което е връхна точка; така ъгълът на фиг. 13 нарича ъгъл В. б) Ако в горната част на различни ъгли, ъглите посочени три букви, които стоят в горната част и двете страни. В този случай, писмото в горната част на постановеното и написано в средата.

На фиг. 13, ъгъла В наречен ъгъл ABC. BA и пр линия - двете страни, както и точка Б - връх на ъгъла.

Така ъгъл ABC е ъгъл В или

ABC = ъгъл ъгъл Б.

Star ugla.Slovo ъгъл znakom∠ заменя понякога.

По този начин, на предходния уравнението изобразяват писане:

В случаите, когато на мястото на излизането на няколко реда в точка Б, има няколко гледни точки.

На фиг. 14 от точка Б се прави линии BA, BC, BD и в горната част на Б, има ъгли ABC, CBD, Абд.

Съседните краища. Две ъгли се наричат ​​съседни, ако имат obscheyu отгоре, една обща и другите две са от двете страни на общата страна.

ABC и CBD ъгли (фиг. 14) са съседни ъгли. Те имат общ връх B, външните страни BC, а другите две бакалавърски и BD лъжата един върху и този по-долу общата страна пр.

Ъглите променят техния размер, ако наклонът се променя от едната страна към другата. От два ъгъла, които имат общ връх, ъгълът, който се вписва в рамките на другия ъгъл, тя се нарича голям ъгъл. Цифрата 14

год. ABD> HS. ABC и HS. CBD <уг. ABD.

За да има концепция за взаимно двете най-големи ъгли, имащи различни върхове, насложени един ъгъл на друг. Когато прилагането им да се съчетаят на върха и надолу едната страна, а другата посока ще позволи да се сравни тяхната стойност. За сравнение на двете ъгли ABC и DEF (Фигура 15). Се прилага на ъгъл ъгъл ABC DEF, така че страната изработен от EF страна BC, точка Д съответствие с точка В; а след това на страна ЕД може да отнеме три позиции, тя може да съвпадне със страна BA, попадат в и извън ъгъл ABC.

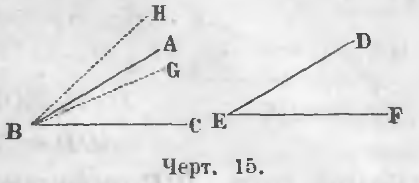
а) Ако линията на ED съвпада с линиите на BA, ъглите се наричат ​​равни

б) Ако линията на ED попада в ъгъла ABC и отнема позиция BG, ъгъл ABC DEF е по-голям ъгъл

год. ABC> HS. DEF.

в) Ако линията на ED попада извън ъгъл ABC по посока BH, ъгъл ABC DEF-малко от ъгъла

год. ABC <уг. DEF.

Събиране, изваждане, умножение и деление на ъгли. Две съседни ABC и ъгъла CBD (Юни. 14) образуват един ъгъл ABC. Ъгъл ABD се нарича сумата от ъглите на ABC и Конвенцията за биологичното разнообразие. Това е изразено в писмена форма с уравнението:

∠ABD = ∠ABC + ∠CBD (а)

От (а) имаме равенство:

т. е. ABC е ъгъл разлика от ъгли Abd и CBD в и ъгълът CBD е разликата между ъглите Abd и ABC.

Ъглите могат да добавят и изваждат.

Ако точка O (фиг. 16) е равна на няколко съседни краища, т. Е. Ако

∠AOB = ∠BOC = ∠COD = ∠DOE,

АОС на ъгъл, равен на сумата от ъглите АОВ и ВОС е два ъгъла АОВ,

∠AOC = ∠AOB + ∠BOC, пътека. ∠AOC = 2AOB.

Ъгъл AOD е три ъгли АОВ

От друга страна, AOB половин ъгъл е свидетелството за авиационен оператор на ъгъл, ъгъл AOD третата четвърт ъгъл AOE.

Други въпроси = Уг АОС = 1/3 AOD = ¼ АОЕ.

От това заключаваме, че ъглите на количествата могат не само да събира и изважда, но и умножение и деление с абстрактно число.

Ако два съседни ъгли ACD и DCB (Юни. 17), двете страни СА и са на една линия, те се наричат ​​съседни.

Съседни ъгли. Съседни ъгли са тези, в които едната страна на общата, а другите два са на една и съща линия.

Ако CD на линията, като се обърна към точката на C, заема длъжността CE, ъгъл ACD намалява привлекателността на ъгъла на АСЕ на и ъгъл BCD увеличаване на жалбата до пр.н.е. ъгъл на. CD линия, продължава да се включите, може да приеме ситуация, в която ще се извърши два съседни ъгъла са равни. Когато два съседни ъгъл ACD и DCB са (Юни. 18), те се наричат ​​прав ъгъл.

В този случай, CD линия се нарича перпендикулярна линия АБ или просто перпендикулярна на линията AB.

В чертежа, 19, изготвен от прав ъгъл без друг съседен на него.

Прав ъгъл е равен на една от съседните ъгли.

Нормалното е права линия, която формира по друг ред точно на ъгъла на.

На чертежа, ъглите 18 и ACD DCB, останалите съседни и равни ъгли получен от заглавието. DC линия ще бъде перпендикулярна на линията AB. Тази взаимна връзка на двете линии, понякога се изразява в писмен вид: CD ⊥ AB.

Тъй като AB линия ще бъде перпендикулярна на диска на линия, линия AB и компактдиска са взаимно перпендикулярни, т. Е. Ако CD ⊥ AB, след AB ⊥ CD.

Единствен перпендикулярно. Взаимна за среща на две перпендикулярни линии, наречен подметки перпендикулярно.

Точка C (Юни. 18) е перпендикулярна единствен CD.

Във всяка точка на AB линия може да се направи перпендикулярна на линията AB.

А перпендикулярна на линията (AB) от гледна точка на линията, след това повишаване до перпендикуляра. Извършване на перпендикуляра (DC) на линията (AB) от точка (D), разположена извън линията, след това да падне перпендикулярна (фиг. 18).

Наклонената права. Всеки ред е не-перпендикулярна на друга линия, наречена се наведе към нея.

На фигурата линия СЕ 20 ще се наклони към линията AB и CD на линия е перпендикулярна на линията AB.

ъгъл на ЕЦБ по-малко директна, но по-голяма от право ACE ъгъл. ЕЦБ нарича остър ъгъл и тъп ъгъл ACE.

Остра ugolest всеки ъгъл по-малък от прав ъгъл. и ugolest тъп ъгъл по-директен.

В същото име, и за разлика от ъглите. Две остър или тъп ъгъл, наречен две едноименния и два ъгъла от които един остър и един тъп наречени противоположно.

Тя представлява наклонена линия CE (фиг. 20) с два съседни прав ъгъл AB от които е по-малко от един, а друг вече права, т. Е. Една остра и един тъп.

Теорема 3. От гледна взето по права линия, можете да набере до него, само един перпендикулярно.

Предвид линия AB и точка на това C (фиг. 20).

Ние трябва да се докаже. че е възможно да се издигне само един перпендикулярно.

Доказателство. Да предположим, че е възможно от точка С до линията AB издигне две перпендикулярни (. 20 Фиг) CD и CE. Чрез собственост на перпендикуляра

год. DCB = ил. ACD (а)
год. Хр = ил. ACE.

Ако приложим на първата част от последния неравенство ъгъла на ранно детско развитие, ние получаваме неравенството

год. Хр + HS. ECD> HS. ACE или HS. BCD> HS. ACE.

Смяна на неравенството у,. ACD BCD равен на ъгъла (а), получаваме

год. DCA> HS. ACE,

неравенство очевидно е абсурдно, тъй като частта, която не може да бъде повече от неговата цялост, откъдето идва и предположението, че може да се повиши до две перпендикулярни, води до абсурд, затова е невярно. В неистинността на предположението, се основава на съображението, че от правилната позиция не може да се извлече погрешно заключение, поради това, нашата теорема е вярно.

Метод за да докаже валидността на тази теорема и посочва невъзможността за абсурдността на някакви други предположения, посочени доказателство начин чрез противоречие или метод за слагане на абсурд.

Теорема 4. Всички прави ъгли са равни.

Да предположим, че има два чифта ъгли: (. 21 функции) един чифт краища представляват ACD и DCB и други ъгли на Е.Г.Х. на HGF и, следователно, CD ⊥ AB и HG ⊥ EF.

Ние трябва да се докаже, че ъглите са равни.

Доказателство. Налагане на линия EF до линията AB точка G до точка C, линията след GH се насочват към интернет CD, тъй като C може да издигне само от една точка на перпендикулярно оттам прав ъгъл ъгъл DCB = директно HGF.

Заключение. Прав ъгъл е постоянна.

Мярка ъгли. При измерване на ъглите на прав ъгъл, както е постоянна величина, да вземе сравнението на единица. Неговата величина е обозначен с букви г.

В такъв случай
всеки остър ъгъл всеки тъп ъгъл> г.

Всички ъгли са изразени с права. Например, че ъгълът е Уг г, 2/3 г и др ...

Теорема 5. Сумата на две съседни ъгли, равни на две прави.

Са съседни ъгли ACD и DCB (фиг. 22).

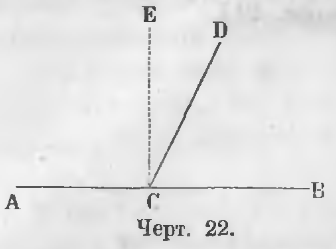
Ние трябва да докаже, че ACD + DCB = 2г.

Доказателство. От гледна С изправени перпендикулярно CE, а след това

ACD = АСЕ + ECD = г + ECD
DCB = ECB - ECD = г - ECD

Добавянето на тези равенства, ние имаме:

ACD + DCB = АСЕ + ECB = 2d (QED).

Следователно два съседни ъгъла добавка един от друг, за да две линии и се наричат ​​допълващи ъгли.

Теорема 5 следва разследването. Една двойка от съседни ъгли е равен на другите две съседни ъгли.

Теорема 6 (обратна теорема 5). Ако сумата от два съседни ъгли е равна на два прави ъгъла, а след това другите две страни са колинеарни.

Нека сумата от два съседни ъгли ACD и DCB е равна на два прави ъгъла (фиг. 23).

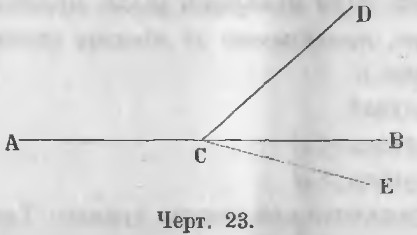
Ние трябва да докаже, че ACB права линия.

Доказателство. Да приемем, че АТБ е прекъсната линия, както и че продължаването на AC линия е CE линия, а след това

Двете стойности са равни на една и съща трета равно (аксиома 3), поради

ACD + DCB = ACD + DCE

които той оставя в намаляването на

Накрая смешна (част, равна на цяло види. Макс. 1), по този начин ACB линия е права линия (както се изисква).

Теорема 7. Сумата на ъглите, които имат връх в един момент и подредени от едната страна на правата линия, е равно на две прави.

ACD дадени ъгли, DCE, ECF, FCG, GCB, имащи общ връх в точка С и разположени от едната страна на линията AB (фиг. 24).

За да се докаже, че

ACD + DCE + ECF + FCG + GCB = 2d.

Доказателство. Ние знаем, че сумата от два съседни ъгли ACF и FCB, равна на две надясно (Vol. 5).

От ACF = ACD + DCE + ECF и FCB = FCG + GCB, подмяна на ъгъла ACF FCB и техните стойности, намираме:

ACD + DCE + ECF + FCG + GCB = 2d (QED).

Теорема 8. Сумата от всички ъгли, разположени около една точка е равна на четири поредни.

Предвид ъгли АОВ, ВОС, COD, DOE, EOA, с общ връх О и разположен около точката O (фиг. 25).

За да се докаже, че

АОВ + ВОС + COD + DOE + EOA = 4d.

Доказателство. ЕО простират към ОГ посока (25 юни), след това

GOB + ВОС + COD + DOE = 2d.

Добавянето на тези равенства, ние имаме:

EOA + AOG + GOB + ВОС + COD + DOE = 4d.

Тъй като AOG + GOB = Други въпроси, на

EOA + АОВ + ВОС + COD + DOE = 4г (QED).

АТБ на ъгъл с DCE и ъгъл ъгъл BCD с вертикален ъгъл нарича ACE (Юни. 26).

Вертикални ъгли. Вертикални ъгли са тези, чиито страни са съставени от една от страните да продължат под друг ъгъл.

Теорема 9. вертикални ъгли са равни.

Има вертикални ъгли (Юни. 26) ACB и DCE, точно както BCD и ACE.

Трябва да се покаже, че ACB = DCE и BCD = АСЕ.

Доказателство. От Теорема 5 имаме равенства:

ACB + BCD = 2d (сумата на две съседни ъгли)
BCD + DCE = 2d

ACB + BCD = BCD + DCE

където, като се махне Равно ъгъл на BCD, ние откриваме

По същия начин, показват, че

Ravnosekuschaya (ъглополовяща) е линията разделяне в половината ъгъл.

На фигурата е 27 ъглополовящата BD ако ∠ABD = ∠DBC.

Теорема 10. ъглополовящи на две съседни ъгли са взаимно перпендикулярни.

Това е съседните ъгли ACB и BCD (Юни. 28). Тяхната разполовяване линии CE и CF разделят съседните ъгли BCD и ВСА половина, следователно BCF = FCD, АСЕ = ECB.

Ние трябва да се докаже, че ЕО ⊥ КФ на

Доказателство. при условие,

ECB = Уг АСВ, BCF = Уг BCD

Добавянето на тези равенства, ние имаме:

ECB + BCF = Уг АСВ + Уг BCD = Уг (АСВ + BCD).

Тъй АСВ + BCD = 2d, на

ECB + BCF = Уг · 2г = г.

Тъй като ЕЦБ + BCF = ECF г.

Ъгъл ECF линия т. Е. CE и CF са взаимно перпендикулярни линии (QED).