Кръг, окръжност, радиус, диаметър, сечащ акорд

Определяне на обиколката на кръга. радиус

Обиколка - равнина локус на еднакво разстояние един от неговите точки (в средата).

Равни сегменти, свързващи централните точки на окръжността се нарича радиус.

Кръгът - равнина част, разположена във вътрешността на кръга.

Диаметърът на акорд дъга

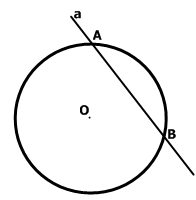
А линията, минаваща през двете точки на окръжността се нарича сечащ. и неговия сегмент лежи в кръга - един акорд. Акорд, минаваща през центъра О, наречена диаметъра. Диаметърът е два пъти радиуса.

Част от дъга от окръжност се нарича.

Дъг нарича полукръг. ако сегментът свързване на краищата, е диаметъра на кръга.

Теорема. Ако два кръга пресичат акорд, след това сегментите на продукта на една струна равнява продукт на различни дължини акорд.

Тангенциално на околната

Tangent - Прав, който има само една обща точка с окръжността.

Теорема. Допирателната към окръжността, перпендикулярна на радиуса провежда до точката на допиране.

Обратна връзка теорема (знак тангента). Ако линията минава през радиуса на края лежи на окръжността и перпендикулярна на този радиус, е допирателна.

Сегментът е част от кръг, ограничена от дъгата и акорда го опираща.

А перпендикулярна съставен от средата на акорда до пресичането с дъгата се нарича дъга стрелка. Дължината на стрелката се нарича височина сегмент.

Сектор е част от кръг, ограничена от два радиуса и дъга, проведено в края на дъгата.

Сектор намеси радиуси образуваща ъгъл от 90 0. наречен квадрант.