Максимални и минимални стойности на функцията - studopediya

Ако функцията е непрекъсната по затворен интервал хÎ[А; Ь]. непременно има в този интервал минималните и максималните стойности (това е едно от свойствата на непрекъснатост на затворения интервал):

Тези стойности са постигнати или функционални екстремум точки в рамките на сегмента, или в крайните точки.

Обикновено практикуват намирането на най-малките и най-големите ценности на функцията на сегмента:

1) намерите критичните точки на интервала;

2) изчисляване на стойностите на функцията намерени в критичните точки;

3) изчисляване на стойностите на функцията на крайните точки, т.е. в точки х = а и х = В;

4) сред всички от изчислените стойности на функцията, за да изберете най-голямата и най-малката.

Ако функцията на х интервалÎ[А; Ь], има само една критична точка и точката на максимална (минимална), след това в този момент на функцията е на най-голямата (малката) стойност.

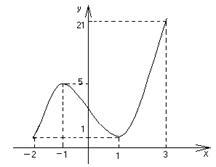
Намерете най-голямата и най-малката стойност на функцията на интервал хÎ[-2, 3].

Тъй като. критичните точки на функцията са x1 = 1 и Х2 = 1 и двете принадлежат към интервала
[-2; 3]. Сравнение на стойностите на функцията на тези точки и стойностите на функцията в краищата на предварително определена дължина

Ние се заключи, че най-малката стойност на функцията е 1, и се постига в точката х = 2 и X = 1 и най-голямата функция стойност е равна на 21 и се постига при х = 3.

Всички резултати са добре илюстрирани със схематична диаграма в даден интервал.

. хÎ[1, е]. Намери и.

На всички точки на тази предварително определена функция на затворен сегмент се определя и непрекъснато, има производно

Както фиксирана точка x1 = 0 и Х2 не принадлежи на интервала [1; е]. Следователно, няма критични точки в рамките на предварително определен интервал (т.е., той запазва функцията монотонност). Остава да се изчисли стойността на функцията в крайните точки:

Шофиране графика на функцията:

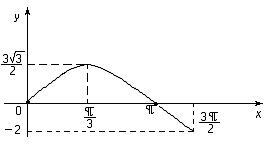
Намерете най-ниските и най-високите стойности на функцията. ,

В този интервал затворен функция е непрекъсната и има производно.

Намираме критичните точки в рамките на предварително определен период:

Þ Û Û

Изчисляваме стойностите на критичните точки и в краищата на интервала:

Шофиране графика на функцията:

В много геометрични, физически и технически задачи, необходими за определянето на максималната и минималната стойност на свързана функционална връзка с друга стойност. За да се реши този проблем, ние трябва, въз основа на неговите условия, изберете независимата променлива и изразяват стойността на изследваните през тази променлива, и след това намерете желаната максимална или минимална стойност на получената функция. В този интервал от независимите променливи промените може да бъде ограничен или безкрайно, също така се определя от условията на проблема.

Определя отворени размери басейн с правоъгълно дъно от 32 m 3, така че стените на линейните и неговото дъно е отишло малко количество материал.

Количеството вещество, необходимо за стените и дъното на басейна се определя от площта на басейн, т.е. стойност (m 2). където

х - е дължината на страните на правоъгълно дъно,

у - е височината на басейна.

Както е фиксирана на обема на басейна. стойностите на х и у не са независими, но са свързани чрез уравнението х 2 Y = 32. , от които ние намираме.

След това, обект на разследването от стойността на района. изразена като функция на един независими променливи X:

Ние разглеждаме тази функция в най-ниската стойност, като се нанасят й зависимост от х:

Þ когато х = 4;

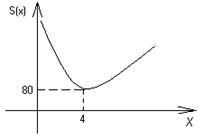
A: басейн размер х m = 4, у = 2 m.

От трите бордовете на същата ширина тясно заварени улей за доставяне на вода. По какъв ъгъл на наклон на страничните стени на улея до дъното на зоната на улея напречно сечение ще е най-голямо?

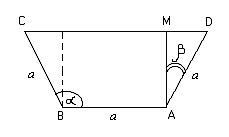
Напречното сечение на улея е на равнобедрен трапец ABCD, в който страничните стени и долната основа равна на ширината на дъските (означени с).

Очевидно е, че този трапец площ зависи от ъгъла на наклона на стените на по-ниска база. Но тук е по-удобно да се въведе като независима променлива ъгъл.

От променлива площ на трапец S може да се запише като функция на ъгъла:

. Î , където, S (0) = а 2 S = 0.

Ние намираме най-голямата стойност на непрекъснато функцията на затворения интервал:

при Û Û

- единствената неподвижна точка в пространството.

Нека да се провери, че това е точката на максимално използване на втората производна:

ако функцията има максимална (вторите достатъчни условия оптималност).

Тъй като това е единственият максимална екстремум в интервала, и то дава най-голяма стойност на функцията.

Намиране. отговаря на условията по този проблем, ние се изчисли.

Намерете най-ниската и максималната стойност на функцията на затворен интервал.