Най-голямата и най-малката стойност на функцията
От практическа гледна точка, най-интересно е използването на деривати, за да открие най-големите и най-малките стойности на функцията. Каква е причината? Максимизиране на печалбата, минимизиране на разходите, определяне на оптималното използване на оборудването. С други думи, в много области на живота е необходимо да се реши проблема с оптимизиране на всички параметри. И това е проблемът с намирането на най-големите и най-малките стойности на функцията.
Трябва да се отбележи, че максималната и минималната стойност на функцията се търси обикновено в X. интервал, която е изцяло или домейн на функция или част от областта на дефиниция. Самостоятелно интервал X може да бъде отворен сегмент интервал безкраен интервал.
В тази статия ще говорим за намиране на максималните и минималните стойности на изрично функция на една променлива у = е (х).
Навигация в страниците.
Най-голямата и най-малката стойност на функция - определение, илюстрацията.
Накратко обсъдят основните определения.
Най-високата стойност на функция у = F (X) в Х интервал се нарича стойност, така че за всяко неравенство.
Най-малката стойност на функция у = F (X) в Х интервал се нарича стойност, така че за всяко неравенство.
Тези определения са интуитивни: най-голямата (най-малката) стойността на функцията - това е най-голямата (най-малката) стойност, получена в интервала на абсцисата.
Неподвижните точки - са стойностите на аргумента, в която производното става нула.
Защо ни е фиксирана точка, когато максималните и минималните стойности? Отговорът на този въпрос е даден от последната теорема на Ферма. От това следва, че ако теорема диференцируема функция има екстремум (локален минимум или локален максимум) в определен момент, след това тази точка е фиксиран. Така, функцията често се своя максимум (минимум) стойност X на интервал в един от фиксирани точки на този интервал.
Също така е често най-голямата и най-малката стойност на функцията може да бъде взето на точките, в които има първата производна на тази функция, както и функцията е дефинирана.
Веднага отговорът на един от най-често задаваните въпроси по темата: "винаги е възможно ли е да се определи най-високата (най-ниската) стойността на функцията"? Не, не винаги. Понякога границата интервал Х съвпада с границите на областта на дефиниция на функция или X на интервал е безкраен. А някои функции на безкрайност и по границите на определенията на полето може да се приема като безкрайно голямо и безкрайно малки стойности. В тези случаи, нищо не може да се каже и за най-високата и най-ниската стойност на функцията.
За по-голяма яснота, ние се даде нагледна илюстрация. Погледнете цифрите - и много по-ясна.
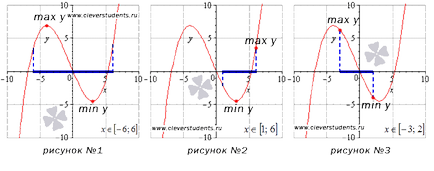
Първата функция на картината се най-високата (максимална Y) и най-малкият (мин Y) стойности при стационарни точки, които са в интервала [-6, 6].
Да разгледаме случая, показан на втората снимка. Промяна на сегмент [1, 6]. В този пример, най-малката стойност се постига при фиксирана точка, а най-голямата - точката с абсцисата, съответстваща на дясната граница на интервала.
Фигура №3 гранични точки на интервала [-3, 2] са абсциси на точките, съответстващи на най-голямата и най-малката стойност на функцията.
В отворен интервал
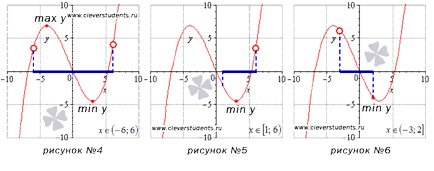
четвърта функция картина се най-високата (максимална Y) и най-малкият (мин Y) стойности в стационарни точки, разположени на открито интервала (-6, 6).
На интервал [1; 6) най-малката стойност на функцията се извършва при стационарен пункт, както и за най-голяма стойност не можем да кажем нищо. Ако точката х = 6 е бил част от интервала, докато при тази стойност на функцията ще отнеме най-голяма стойност. Този пример е показан на Фигура №5.
Фигура №6 малката стойност се постига в дясната граница на интервала (-3 ;. 2] може да се направи най-голямата стойност на заключения.
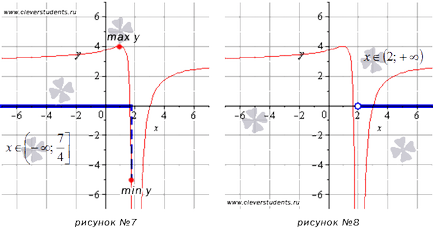
В примера, показан на седмия фигурата, функцията се най-високата стойност (макс у) в неподвижна точка с абсциса х = 1. и най-малката стойност (мин у) се постига от дясната граница на интервала. При стойности на минус безкрайност асимптотично приближава у = 3.
Функцията за интервал не достига най-малките или най-голяма стойност. Когато стремеж за х = 2 надясно стойности функция са склонни да минус безкрайност (права линия х = 2 е вертикален асимптота) и абсцисата тенденция да плюс безкрайност, стойностите на функцията асимптотично приближаващи у = 3. Графичен илюстрация на този пример, е показан на Фигура №8.
Алгоритъмът за намиране на най-големите и най-малките стойности на непрекъсната функция в интервала [а, Ь].
Пишем алгоритъм за намиране на най-голямата и най-малката стойност на функцията на интервал.
- Виж областта на функцията, и проверява дали то целия интервал [а, Ь].
- Намери всички точки, в които има първата производна и които се съдържат в интервала [а, Ь] (обикновено в тези точки vstechayutsya функция с аргумент на знака модул и електрически функции с фракционна-рационално индикатор). Ако тези точки не са, тогава ние да преминете към следващата стъпка.
- Определя всички неподвижни точки, които попадат в интервала [а, Ь]. За да направите това, ние откриваме, производната на функцията. приравнявайки го до нула, и решаване на полученото уравнение изберете подходящия корен. Ако няма стационарни пункта, или никой от тях не пропуска разреза, след това преминете към следващата стъпка.
- Ние изчисляване на стойностите на функцията в избраните фиксирани точки (ако има такива) в точките, в които няма първата производна (ако има такива), и когато X = О и X = б.
- От получените стойности на функцията, изберете най-голямата и най-малката - те са необходими и минимални и максимални стойности на функцията съответно.
Нека разгледаме алгоритъма за решаване на примера на намиране на най-големите и най-малките стойности на интервала.
Намерете най-голямата и най-малката стойност на функцията- в интервала [1, 4];
- в интервала [-4, -1].
Нека да започнем с домейна на функцията. Квадратичен полином в знаменателя не изчезне:

Лесно е да се провери дали всички интервалите на условията на проблема принадлежат към областта на функцията.
Очевидно е, че съществува производната в цялата област на функцията.
Намираме стационарни точки. Производно изчезва при. Тази неподвижна точка попада в интервалите (-3, 1] и (-3, 2).
За първи период изчисли стойността на функцията на х = -4 и ограничение на безкрайност минус:
От тогава, а на най-малко стойността на функцията на изводи могат да се направят. Може да се каже, че само стойностите на функция са ограничени по-долу със стойност от 1 (функция стойност минус безкрайност асимптотично подходи права линия у = 1).
Вторият интервал на интереси, който не съдържа стационарна точка, и нищо от това не е строга граници. В този случай, не можем да намерим най-голямата или най-малката стойност на функцията. Изчисляване на срока на минус безкрайност и аргументът клони към минус три отляво, ние ще бъдем в състояние да определи границите на стойностите на само:
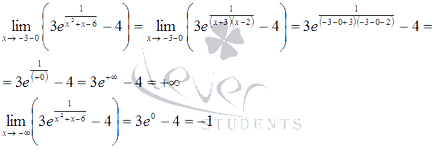
Следователно, стойностите на функцията са в диапазона от X в празнината.
За третия период (-3, 1] се изчисли стойността на функцията на стационарна точка и когато х = 1 и едностранно ограничение, аргументът тенденция да -3 полето :.
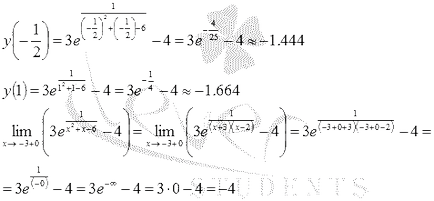
Следователно, най-голямата стойност в този интервал функцията се в стационарна точка, най-малката стойност на функцията, не можем да се изчисли, но стойността на функцията е ограничена отдолу от -4.
За интервала (-3, 2) да използват резултатите от предходния параграф, и по-нататък се изчисли двустранен лимит има тенденция да Deuce ляво:
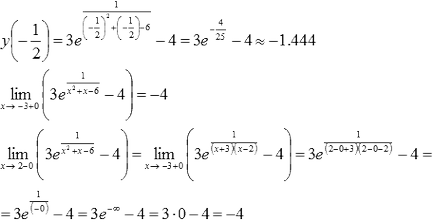
Следователно, най-малката стойност не е възможно да се определят стойностите на функциите са ограничени отдолу от -4.
Резултатите от предходните две точки показват, че в интервала [1; 2) получава най-голямата стойност на функцията при х = 1. най-малката стойност не може да бъде намерен, стойностите на функциите са ограничени отдолу от -4.
Функцията за интервал не достига нито най-голямата или най-малката стойност.
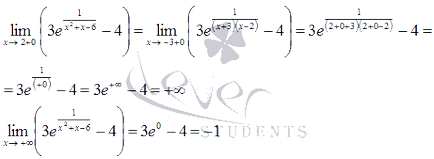
Това означава, че в този диапазон приема стойности в интервала.
Изчисляване на стойността на функцията при х = 4. може да се твърди, че в функция плюс безкрайност асимптотично подходи права линия у = 1.
Сега можете да сравните получените резултати във всяка точка с графиката на функцията. Сините пунктирани линии показват асимптотата.
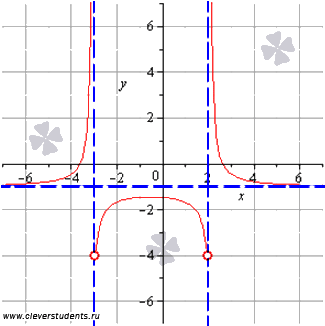
На тази можете да се окажете с намирането на най-големите и най-малките стойности на функцията. Алгоритмите разбират тази статия, позволяват да се получат резултати с минимално действие. Въпреки това, е полезно да се определи първо интервалите на увеличаване и намаляване на функцията и едва след това да се направят изводи за най-високата и най-ниската стойност на функцията на всеки интервал. Това дава по-ясна картина и строга обосновка на резултатите.