Радиусът кръг с диаметър, пи, сектор, допирателната

Radius. разстояние от центъра на кръга на нейните граници.

Диаметър. най-голямо разстояние от един периферен ръб на друг. Диаметърът е два пъти радиуса.

Периметър (обиколката). обиколка граница.

Обиколка $ = \ пи \ пъти $ диаметър

Дъг. извита линия, която е част от окръжност.

Arc измерва в градуси или радиани. Например: 90 °, или $ \ Frac $ - четвърт кръг, 180 ° или $ \ пи $ - половината от кръга.
Сумата на всички дъги е 360 °

Акордът. отсечка, свързваща две точки върху кръга.

Сектор. като парче торта (клин).

Допирателната към окръжността: правата линия, перпендикулярна на радиуса, и имат само една обща точка от okurzhnostyu.

Обиколка $ = \ пи \ cdot \ текст = 2 \ cdot \ пи \ cdot \ текст $

кръг площ $ = \ пи \ cdot $ 2 диапазон

Радиусът означен като R. като г диаметър. P като обиколката и областта на двете S.

$ Р = \ пи \ cdot г = 2 \ cdot \ пи \ cdot R $
$ S = \ пи \ cdot R ^ 2 $

Площ на сектор кръг, K. (с централен ъгъл $ \ тета $ и радиус R $ $ в).
Ако ъгъл $ \ тета $ в градуси, тогава площ = $ \ Frac \ пи R ^ 2 $
Ако ъгъл $ \ тета $ в радиани, тогава област, тогава областта = $ \ Frac R ^ 2 $

Ако дължината на дъга е $ \ тета $ окачествяване или радиани, стойността на централния ъгъл като $ \ тета $ (градуси или радиани).

(. В инчове, разпределителни гари, крака, инча, m) Ако знаете дължината на дъгата може да намерите стойността на съответния му централен ъгъл ($ \ тета $) с помощта на формулата:

вписан ъгъл

Вписан ъгъл е ъгълът на върха на обиколката и със страни, които съдържат хордата на кръга.
На фигурата ъгъл APB е вписан ъгъл.

Стойността на вписан ъгъл е половината от дъгата, на които тя разчита.

например:
$ \ Widehat = 84 ^ \ Circ $
$ \ Angle APB = \ Фрак = 42 ^ \ циркулационната $

Случай 1: двете secants се пресичат вътре обиколка.

Когато две secants пресичат в кръга, стойността на ъгъла, образуван от два пъти по-малки от стойностите на дъгите на които се основават. Фигура дъга дъга АВ и CD са 60 ° и 50 ° ъгли докато 1 и 2 са равни $ \ Frac (60 ^ \ Circ + 50 ^ \ Circ) = 55 ^ \ Circ $

Случай 2: две пресичащи се пресичат извън кръга.

Понякога пресичащи се пресичат извън кръга. Когато това се случи, размера на получената ъгълът е равен на половината от разликата между дъгите на които се основават.

$ \ Ъгъл ABC = \ Frac (х - у) $

фигура дъга AB = 80 ° и дъга CD = 30 °.
$ \ Ъгъл ABC = \ Frac (80-30) = \ Frac \ cdot 50 = 25 ^ \ Circ $

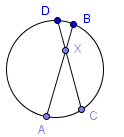
Ако двете акорди се пресичат вътре обиколка, както е показано по-горе, след това:

$ AX \ cdot XB = CX \ cdot XD $